Объяснение:
меньшая сторона=5
большая сторона 13
необходимо упаковок 2
1) х² - 9х+14 = 0
Выделим полный квадрат: х² - 9х+14 = х² - 2*4,5х + 4,5² - 4,5² +14 =
= (х - 4,5)² - 20,25 + 14 = (х - 4,5)² - 6,25 = (х - 4,5)² - 2,5² =
= (х - 4,5 - 2,5)(х - 4,5 + 2,5) = (х - 7)(х - 2) => уравнение имеет вид:
(х - 7)(х - 2) = 0
х - 7 = 0 или х - 2 = 0
х = 7 или х = 2
ответ: 2; 7.
2) х²+5х - 14 = 0
Выделим полный квадрат: х²+5х - 14 = х² + 2*2,5х + 2,5² - 2,5² - 14 =
= (х + 2,5)² - 6,25 - 14 = (х + 2,5)² - 20,25 = (х + 2,5)² - 4,5² =
= (х + 2,5 - 4,5)(х + 2,5 + 4,5) = (х - 2)(х + 7) => уравнение имеет вид:
(х - 2)(х + 7) = 0
х - 2 = 0 или х + 7 = 0
х = 2 или х = -7
ответ: 2; - 7.
5 см и 12 см
Объяснение:
пусть стороны прямоугольника равны х и у (х,у>0).
тогда по условию:
х² + у² = 13²,х*у = 60.Решаем:
х² + у²=169,
ху=60;
х² + у²=169,
у=60/х;
х²+(60/х)²=169, (1)
у=60/х;. (2)
1. х² + 3600/х² = 169 |*х²
х⁴ + 3600 = 169х²
х⁴ - 169х² + 3600 = 0
пусть х²=t≥0
тогда t² - 169t +3600 = 0
D = (-169)² - 4*1*3600 = 28561 - 14400 =
= 14161 = 119²
t1 = (-(-169)+119) / (2*1) = (169+119)/2 = 288/2 = 144
t2 = (-(-169)-119) / (2*1) = (169-119)/2 = 50/2 = 25
выход из замены:
t=x², x>0
t1 = 144 = x², x1=√144 = 12,
t2 = 25 = x², x2=√25 = 5;
2. y=60/x
y1 = 60/x1 = 60/12=5
5y2 = 60/x2 = 60/5=12
То есть стороны прямоугольника: 5 и 12 см.
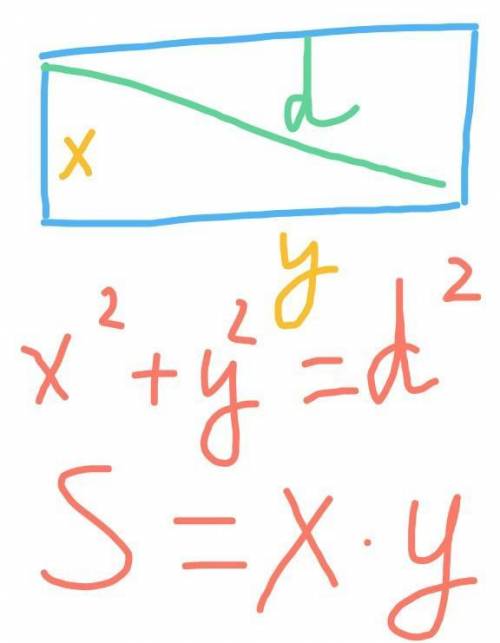
5м, 13 м, 2 упаковки.
Объяснение:
Пусть длина площадки х м, тогда ширина х-8 м.
х(х-8)=65; х²-8х-65=0; по теореме Виета х=-5 (не подходит) х=13.
Длина площадки 13 м, ширина 13-8=5 м.
Р=2(13+5)=36 м.
36:25=1,44 - нужно купить 2 упаковки бордюра
ответ: 5м, 13 м, 2 упаковки.