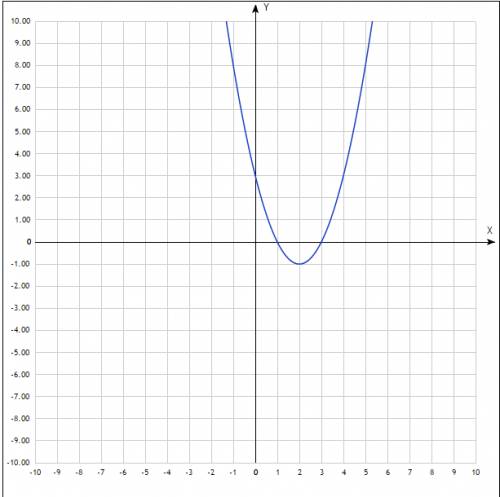
Постройте график функции у = - 2х + 3. По графику найдите:
a) значения функции при значениях аргумента, равных -2; 0; 3.
б) значения аргумента, при которых значения функции равны 3; 7.
в) найдите точку пересечения данной прямой с прямой, заданной уравнением у=5.
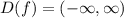
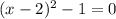
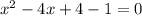
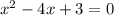
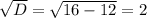
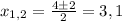
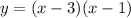
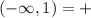
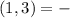
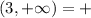
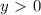 , если
, если 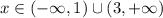
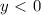 , если
, если 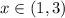
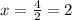
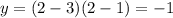
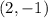
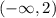
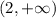
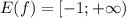
1)V(x+9) =x-3
ОДЗ:
{x+9>=0; x>=-9
{x-3>=0; x>=3
Решение ОДЗ: x>=3
Т.к. обе части уравнения неотрицательны, возведем их в квадрат:
x+9= (x-3)^2
x+9= x^2-6x+9
x+9-x^2+6x-9=0
-x^2+7x=0
x^2-7x=0
x(x-7)=0
x=0; x=7
x=0 нам не подходит по ОДЗ
ответ:{7}
2)V(x-2)= V(x^2-4)
ОДЗ:
{x-2>=0; x>=2
{x^2-4>=0; x<=-2, x>=2
Решение ОДЗ: x>=2
Возведем в квадрат обе части:
x-2=x^2-4
x-2-x^2+4=0
-x^2+x+2=0
x^2-x-2=0
D=(-1)^2-4*1*(-2)=9
x1=(1-3)/2=-1 - не подходит по ОДЗ
x2=(1+3)/2=2
ответ:{2}
3)V(12+x^2) <6-x
В левой части неравенства стоит корень,принимающий только неотрицательные значения. Следовательно, и правая часть должна быть положительной.
ОДЗ:
{12+x^2>=0 при x e R
{6-x>0, x<6
Решение ОДЗ: x<6
Возведем в квадрат обе части:
12+x^2<(6-x)^2
12+x^2<36-12x+x^2
12+x^2-36+12x-x^2<0
12x-24<0
12x<24
x<2
С учетом ОДЗ: x <2