11.25 м, 1/12 м/с²
Объяснение:
Известно, что скорость - производная от пути, поэтому путь - это интеграл от скорости. Пусть s(t) - функция пути. Тогда
![s(t)=\int{v(t)dt}=\int{\sqrt[3]{1+t}dt}\\](/tpl/images/1307/5318/d41d8.png) .
.
Пусть u = 1+t, тогда du = dt.
![\int{\sqrt[3]{1+t}}\,dt=\int{\sqrt[3]{u}}\,du=\int{u^\frac{1}{3}}\,du=\frac{u^{1/3\,\,\,+\,\,\,1}}{1/3\,\,\,+\,\,\,1}+C=\frac{u^{4/3}}{4/3}+C=\frac{3}{4}u^{4/3}=\frac{3}{4}\sqrt[3]{u^4}+C](/tpl/images/1307/5318/e2420.png)
Подставим обратно u=1+t
![\frac{3}{4}\sqrt[3]{u^4}+C=\frac{3}{4}\sqrt[3]{(1+t)^4}+C=s(t)](/tpl/images/1307/5318/c323b.png)
Также, поскольку
![s(0)=\frac{3}{4}\sqrt[3]{(0+1)^4}+C=\frac{3}{4}\sqrt[3]{1}+C=\frac{3}{4}+C=0](/tpl/images/1307/5318/87613.png)
то С=-3/4 (потому что s(0) должно равнятся 0).
По этому
![s(t)=\frac{3}{4}\sqrt[3]{(1+t)^4}-\frac{3}{4}](/tpl/images/1307/5318/aa36e.png) .
.
Ну вот! Теперь у нас есть функция пути. По этому чтобы нати путь который преодолела точка за первые 7 секунд, мы просто находим
s(7).
![s(t)=\frac{3}{4}\sqrt[3]{(1+7)^4}-\frac{3}{4}=\frac{3}{4}\sqrt[3]{8^4}-\frac{3}{4}=\frac{3}{4}(16)-\frac{3}{4}=12-\frac{3}{4}=11\frac{1}{4}=11.25](/tpl/images/1307/5318/0c02a.png)
То есть ответ: 11,25 м.
Дальше, чтобы найти ускорение точки при t=7, возьмем производную от v(t) и подставим t=7.
![v'(t)=\frac{d}{dt}(\sqrt[3]{1+t})=\frac{d}{dt}((1+t)^\frac{1}{3})=(\frac{1}{3}(1+t)^{-\frac{2}{3}})(\frac{d}{dt}(1+t))=\frac{1}{3}(1+t)^{-\frac{2}{3}}=\frac{1}{3(1+t)^{2/3}}](/tpl/images/1307/5318/3f098.png)
Теперь найдем v'(7)
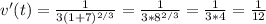
То есть ответ: 1/12 м/с².
48 квадратных сантиметров
Объяснение:
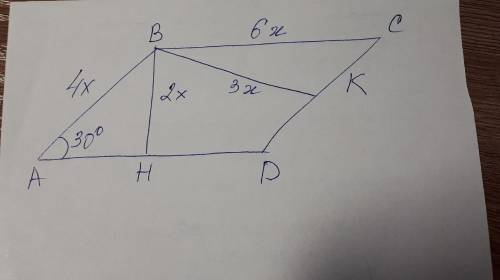
1) Примем одну высоту параллелограмма за 2х (на рисунке это сторона BH), тогда вторую высоту примем за 3х (на рисунке это сторона BK).
2) Поскольку катет против угла в 30° равен половине гипотенузы, то из треугольника АВН получаем, что гипотенуза АВ = 4х.
3) Далее рассмотрим треугольник ВСК. Получаем, что сторона ВС= 6х
4) Затем вычислим периметр параллелограмма: (4х+6х)*2=40 сантиметров
5) 20х=40, откуда х=2
6) Таким образом, можно сделать вывод, что одна сторона 4х=4·2=8 см.
7) Высота проведенная к этой стороне 3х=3·2=6 см
8) Таким образом получаем, что площадь параллелограмма равна 8*6=48 квадратных сантиметров
(x;y)=(3;5)
Объяснение:
Не совсем ровно, но как смогла