3. Пусть A(x; y) - заданная точка.
По условию y = 3. Чтобы найти x, нужно y подставить в уравнение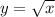 
:
.
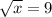Очевидно, что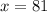 
, поскольку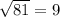 
ОТВЕТ: 81.
5. Очевидно, что общее число процентов должно равняться 100.
Пусть искомая относительная частота равна х.
Тогда 4 + 0 + 8 + x + 12 + 24 + 20 + 16 + 4 = 100;
x + 88 = 100 ⇒ x = 12.
ОТВЕТ: 12%.
6. Упростим выражение:
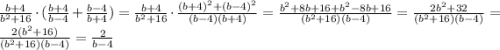
Подставляем b= 3,75:
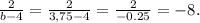
ОТВЕТ: -8.
7. Упростим отдельно числитель и знаменатель:
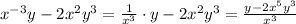
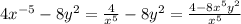
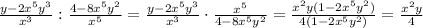
ОТВЕТ: (x²y)/4
8. Пусть x км/час - скорость почтового поезда. Тогда скорость скорого поезда - (x + 20) км/час.
Время, которое затратит скорый поезд на 280 км, равно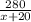 
, а время, которое затратит почтовый поезд на 300 км, равно 
.
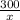По условию время , затраченное почтовым поездом, на 2 часа больше, чем время, затраченное скорым, поездом, т.е. имеем уравнение
;
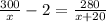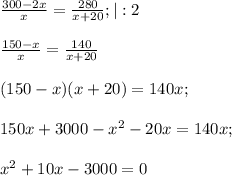
По теореме Виета находим два корня: x = -60 и x = 50. Очевидно, первый по смыслу задачи не подходит, поэтому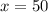 
(км/час) - искомая скорость почтового поезда.
ОТВЕТ: 50 км/час.
Объяснение:
Чтобы не путать русскую букву "З" с цифрой "3" - запишем пример в виде:
R A Z
+
A Z
+ Z
______
4 4 4
1)
Получили, что
Z + Z + Z = 4; 3×Z = * 4
Здесь один вариант: Z = 8: 3×4 = 24
2)
Из разряда единиц переносим двойку в разряд десятков.
Получим:
2 + 2×A = *4
Простым подбором получаем;
A = 1; 2 + 2×1 = 04
A = 6; 2 + 2×6 = 10
То есть если нет переноса в разряд сотен, то
R + 0 = 4; R = 4
Если есть, то:
R + 1 = 4; R = 3.
Возвращаемся к прежним обозначениям.
Получили 2 ответа:
Медианой ряда чисел называется число, стоящее посередине упорядоченного по возрастанию ряда чисел (в случае, если количество чисел нечётное). Если же количество чисел в ряду чётно, то медианой ряда является полусумма двух стоящих посередине чисел упорядоченного по возрастанию ряда.
Упорядочим: 8 8 10 11 11 12
Медиана: (10+11)/2=21/2=10,5