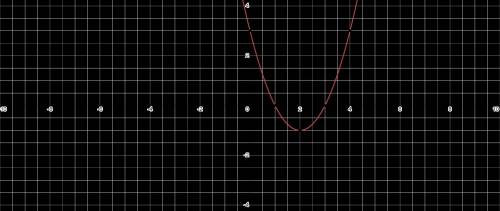
(РИС.1)
Корнями (нулями) являются значения x, в которых график пересекает ось абсцисс (ось X). Для определения корней (нулей) подставляем 0 вместо y и решаем относительно x. Х1= 3, Х2= 1.
Построим график параболы, используя направление ветвей, вершину, фокус и ось симметрии.
Направление: направлено вверх
Вершина: (2,−1)
Фокус:
(2,−3/4).
Ось симметрии:
x=2
Направляющая:
y=−5/4
x 0 1 2 3 4
y 3 0 −1 0 3
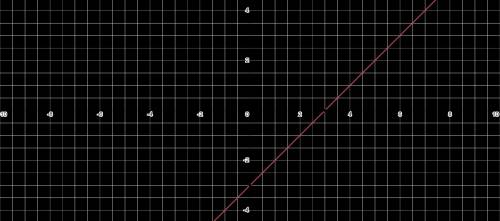
(РИС.2)
Построим прямую с углового коэффициента и пересечения с осью Y или опираясь на две точки.
Угловой коэффициент: 1
Пересечение с осью Y: (0,−3)
x 0 3
y −3 0
Объяснение:
ответ: 1 и -3
Объяснение: Приведенное квадратное уравнение можно решить по т. Виета. Приведенное квадратное уравнение — это уравнение, в котором коэффициент перед x² равен единице.
Теорема, обратная теореме Виета, гласит: если числа x1 и x2 таковы, что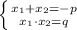
то x₁ и x₂ — корни квадратного уравнения Уравнение х²+2х-3=0 – приведенное.
х₁+х₂=-2
х₁•х₂=-3.
корнями уравнения являются числа 1 и -3, т.к. их сумма 1+(-3)=-2, а произведение 1•(-3)=-3