а)Координаты точки пересечения прямых (2; 5)
Решение системы уравнений (2; 5);
б)Координаты точки пересечения прямых (1; -2)
Решение системы уравнений (1; -2);
в)Координаты точки пересечения прямых (4; 2)
Решение системы уравнений (4; 2);
г)Координаты точки пересечения прямых (4,5; 7)
Решение системы уравнений (4,5; 7)
Объяснение:
Решить систему уравнений графически:
а)у-2х=1
6х-у=7
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
у-2х=1 6х-у=7
у=1+2х -у=7-6х
у=6х-7
Таблицы:
х -1 0 1 х -1 0 1
у -1 1 3 у -13 -7 -1
Согласно графика, координаты точки пересечения прямых (2; 5)
Решение системы уравнений (2; 5);
б)7х-3у=13
х-2у=5
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
7х-3у=13 х-2у=5
-3у=13-7х -2у=5-х
у=(7х-13)/3 2у=х-5
у=(х-5)/2
Таблицы:
х -2 1 4 х -1 1 3
у -9 -2 5 у -3 -2 -1
Согласно графика, координаты точки пересечения прямых (1; -2)
Решение системы уравнений (1; -2);
в)х+у=6
3х-5у=2
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
х+у=6 3х-5у=2
у=6-х -5у=2-3х
5у=3х-2
у=(3х-2)/5
Таблицы:
х -1 0 1 х -1 0 4
у 7 6 5 у -1 -0,4 2
Согласно графика, координаты точки пересечения прямых (4; 2)
Решение системы уравнений (4; 2);
г)4х-у=11
6х-2у=13
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
4х-у=11 6х-2у=13
-у=11-4х -2у=13-6х
у=4х-11 2у=6х-13
у=(6х-13)/2
Таблицы:
х -1 0 1 х -1 0 1
у -15 -11 7 у -9,5 -6,5 -3,5
Согласно графика, координаты точки пересечения прямых (4,5; 7)
Решение системы уравнений (4,5; 7).
среднее арифметическое это число, равное сумме всех чисел множества, делённой на их количество.
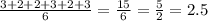
Мода это значение во множестве наблюдений, которое встречается наиболее часто
мода равна 2 и 3 т.к оба встречаются 3 раза
размах называется разность между наибольшим и наименьшим из чисел этого ряда.
наибольшее 3, наименьшее 2
3-2=1
Медиана - это значение приходящееся на середину ряда, расположенного в порядке возрастания или убывания числовых значений признака,
сначала разместим числа в порядке возрастания
2,2,2,3,3,3
видно что чисел шесть тогда медиана равна среднему аримфметическому двух средних чисел
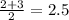
(если допустим было нечетное количество тогда медиана была равна среднему числу. Пример 2,2,2,3,3,3,3 - медиана равна 3)
y'=4/x²
y'(x0)=4/4=1
y'(x0)=tgA=1
A=45°