Упростить выражение:
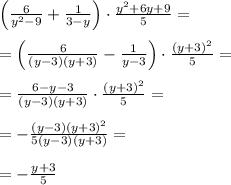
Задача: Два автомобиля выезжают одновременно из одного города в другой, находящийся на расстоянии 560 км. Скорость первого на 10 км больше скорости второго, и поэтому первый автомобиль приезжает на место на 1 час раньше другого. Определить скорость каждого автомобиля.
Пусть скорость второго автомобиля — х км/ч, тогда скорость первого — х+10 км/ч. Второй был в пути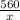 
часов, а первый — 
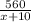часов. Зная, что второй автомобиль был в дороге дольше на 1 час, составим и решим математическую модель:
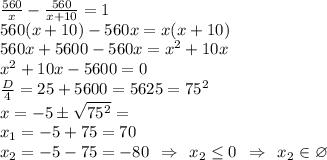
Скорость второго автомобиля — х = 70 км/ч, скорость первого — х+10 = 70+10 = 80 км/ч
скорость первого автомобиля — 80 км/ч;скорость второго автомобиля — 70 км/ч.Задача: При каких значения x функция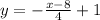 
принимает положительные значения.
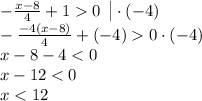
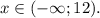
ответ: x < 12 или x ∈ (−∞; 12).
пусть v км/ч - собственная скорость лодки, a s - расстояние между пристанями а и в.
по течению против течения
расстояние, км s s
скорость, км/ч v+3 v-3
время, ч. s/(v+3) s/(v-3)
средняя скорость рассчитывается по формуле:
в нашем случае:
по теореме виета:
(не подходит)
ответ: собственная скорость лодки 9 километров в час.
11c+5 < 7c-7
11c-7c < -7-5
4c < -12|:4
c < -3