Точки построения графика: (0;0), (±1; ±1), (±2; ±8). График является нечетной.
Подставим координаты точки A(-5;125) в график уравнения, получим
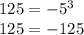
Поскольку равенство не верно, то график функции y = x³ не проходит через точку A(-5;125), т.е. точка не принадлежит графику y = x³
Подставим теперь координаты точки B(4;64), получим
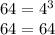
Поскольку равенство тождественно выполняется, то точка B принадлежит графику функции y = x³.
Подставим координаты точки C(-3;-27), имеем
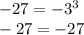
Раз равенство тождественно выполняется, то точка C(-3;-27) принадлежит графику функции y = x³
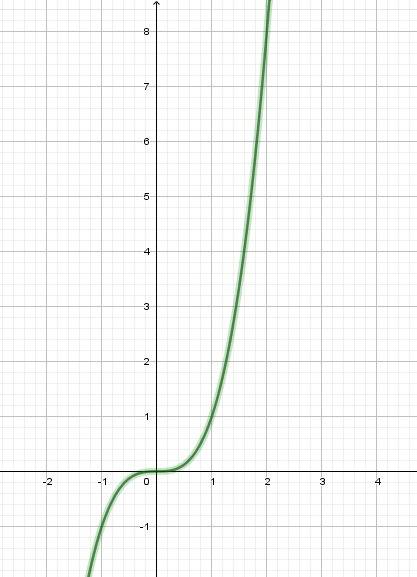
В решении.
Объяснение:
Задайте формулой функцию график которой проходит через точку
(0; 5) и параллелен графику функции у= -4х.
Дана функция: у = -4х;
Точка (0; 5);
Написать формулу функции, параллельной данной.
Графики линейных функций параллельны, если: k₁ = k₂, а b₁ ≠ b₂.
Значит, k₂ = -4;
Найти b₂ ( b₁ = 0):
Подставить в уравнение линейной функции у = kx + b известные значения х и у (координаты точки ) и вычислить значение b₂:
5 = -4 * 0 + b
5 = 0 + b
b₂ = 5;
Формула функции, параллельной данной: у = -4х + 5.