
1) Обозначим первую цифру задуманного числа х, а вторую - у. Выполнив указанные действия, получим:
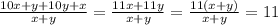
Т.е., всегда будет получаться 11.
2) Признак делимости на 3: на три делятся те числа, сумма цифр которых делится на 3.
Данное число (10^n+317) будет состоять из единицы, n нулей, тройки, единицы и семёрки. Сумма цифр равна 1+3+1+7 = 12.
12 делится на 3, значит, и число 10^n+317 тоже делится на 3, ЧТД
Аналогично, признак делимости на 9: на 9 делятся те числа, сумма цифр которых делится на 9.
10^n состоит из единицы и n нулей. Если от него отнять 1, оно будет состоять из девяток. Соответсвенно, сумма цифр этого числа поделится на 9, ЧТД.
202
Объяснение:
y=x³-75x+20; [-7;0]
y'=3x²-75;
y'=0;
3x²-75=0; 3x²=75; x²=75/3=25; x=±√25=±5'
Абсциссы точек экстремума: x₁=-5: x₂=5.
x₂ не входит в исследуемый отрезок. Определяем характер экстремума в т. x₁=5.
Возьмем вторую производную ф-ии:
y''=(y')'=(3x²-75)'=6x
y''(5)=6*5=30>0 ф-ия в этой точке имеет минимум! Следовательно
В задаче не спрашивается о наименьшем значении ф-ии. Все, что в скобках{...} можно не писать:
{ Наименьшее значение ф-ии - в точке минимума:
y=x³-75x+20;
y(5)=5³-75*5+20=125-375+20=145-375=-230 }
Наибольшее значение ф-ии где-то по концам отрезка:
y=x³-75x+20;
y(-7)=(-7)³-75*(-7)+20=-343+525+20=202;
y(0)=0-0+20=20