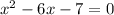
Значение квадратного уравнения.
Решение:для 8 класса (через дискриминант):
Вспоминаем вид уравнения, при котором можно вычислить дискриминант: 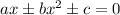 .
.
То есть наше уравнение 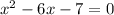 , где
, где 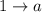 ,
, 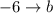 и
и 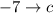 .
.
Вспоминаем формулу нахождения дискриминанта: 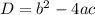 .
.
⇒ 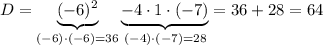
Вы (очень надеюсь) знаете, что есть правила дискриминанта:

Поскольку 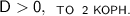
Вспоминаем формулу нахождения корней уравнения:
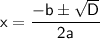 ⇒ Найдём корни нашего уравнения:
⇒ Найдём корни нашего уравнения:
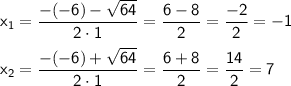
для 7 класса (через разложение трёхчлена):
Представим член 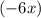 в виде выражения
в виде выражения 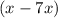 и запишем его в уравнение:
и запишем его в уравнение:
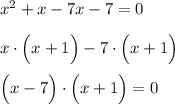
Произведение равно 0, если один из множителей равен 0.
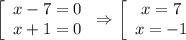
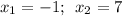 .
.
Дано: bn – геометрическая прогрессия;
b1 + b2 = 30, b2 + b3 = 20;
Найти: b1; b2; b3 - ?
Формула члена геометрической прогрессии: bn = b1 * q^(n – 1),
где b1 – первый член геометрической прогрессии, q – её знаменатель, n – количество членов прогрессии этой формулы выразим второй и третий члены заданной прогрессии:
b2 = b1 * q^(2 – 1) = b1 * q;
b3 = b1 * q^(3 – 1) = b1 * q^2.
Т.о. имеем:
b1 + b2 = 30; и b2 + b3 = 20;
b1 + b1 * q = 30; b1 * q + b1 * q^2 = 20;
b1 (1 + q) = 30; b1 (q + q^2) = 20;
b1 = 30 / (1 + q). b1 = 20 / (q + q^2).
Т.е. 30 / (1 + q) = 20 / (q + q^2);
30 * (q + q^2) = 20 * (1 + q);
30q + 30q^2 = 20 + 20q;
30q^2 + 10q – 20 = 0;
D = (10)^2 – 4 * 30 * (-20) = 2500; sqrt(D) = sqrt (2500) = 50;
q1 = (-10 + 50) / 60 = 2/3;
q2 = (-10 - 50) / 60 = -1.
Подставим оба полученных значений q выражение для нахождения b1:
b1 = 30 / (1 + 2/3) = 30 / (5/3) = 90/5 = 18;
b1 = 30 / (1 + (-1)) = 30 / 0 – смысла не имеет, следовательно, q = 2/3.
b2 = b1 * q = 18 * 2/3 = 12;
b3 = b1 * q^2 = 18 * 2/3^2 = 8.
ответ: b1 = 18; b2 = 12; b3 =8.
Объяснение:
ответ на фото.........