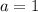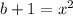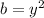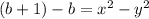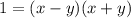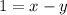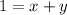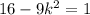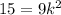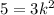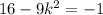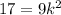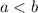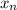 } называется ограниченной сверху, если существует такое число M∈R , что для любого номера n,
} называется ограниченной сверху, если существует такое число M∈R , что для любого номера n, 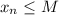 , Последовательность {
, Последовательность {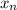 } называется ограниченной снизу, если существует такое число m∈R, что для любого номера n,
} называется ограниченной снизу, если существует такое число m∈R, что для любого номера n,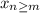 , Последовательность {
, Последовательность {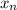 } называется ограниченной, если она ограниченная сверху и ограниченная снизу, то есть существует такое число M>0, что для любого номера n, l
} называется ограниченной, если она ограниченная сверху и ограниченная снизу, то есть существует такое число M>0, что для любого номера n, l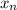 l
l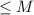 , Последовательность {
, Последовательность {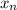 } называется неограниченной, если существует такое число M>0 , что существует такой номер n , что l
} называется неограниченной, если существует такое число M>0 , что существует такой номер n , что l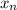 l
l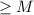
 (1)
(1)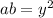 (2)
(2)