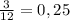 - яйца
- яйца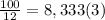 - масла (округлим до 8,5)
- масла (округлим до 8,5)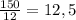 - сахара
- сахара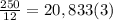 - муки (округлим до 21)
- муки (округлим до 21)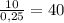 - макс. кол-во маффинов, на которые хватит яиц.
- макс. кол-во маффинов, на которые хватит яиц.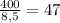 - макс. кол-во маффинов, на которое хватит масла.
- макс. кол-во маффинов, на которое хватит масла.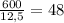 - макс. кол-во маффинов, на которое хватит сахара.
- макс. кол-во маффинов, на которое хватит сахара.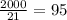 - макс. кол-во маффинов, на которое хватит муки.
- макс. кол-во маффинов, на которое хватит муки.
Наше уравнение вообще имеет решения только тогда, когда дискриминант биквадратного трёхчлена неотрицателен, при этом, в силу чётности биквадратного уравнения, удобно находить чётный дискриминант через половину среднего коэффициента и без множителей в последнем слагаемом, т.е. по формуле
Уравнение не может стать просто квадратным, оно всегда будет иметь старшей степенью 4, поскольку старший коэффициент фиксирован и равен единице. Но биквадратное уравнение может выродится, когда его дискриминант равен нолю, что происходит при
Когда дискриминант больше нуля и биквадратное уравнение не вырождено, то квадратов искомых корней
Левый же квадрат искомых корней отрицателен тогда и только тогда, когда этот левый квадрат лежит левее оси ординат, т.е. левее точки
Отсюда:
О т в е т :