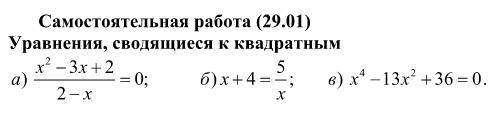
5
2^(x^2-8x+19) > 16
2^(x^2-8x+19) > 2^4
так как основание больше 1 то знак не меняем
x^2-8x+19 > 4
x^2-8x+15 > 0
D = 64 - 60 = 4
x12=(8+-2)/2=5 3
(x-3)(x-5) > 0
метод интервалов
(3) (5)
x ∈(-∞ 3) U (5 + ∞)
7
(x²-8x+16)^(x-6) < 1
((x-4)^2)^(x-6) < (x-4)^0
проверим когда основание равно 0 x=4
степень (х-6)<0 значит х=4 не корень
так как основание слева всегда больше 0 то рассмотрим 2 случае
1. основание >0 и <1
x∈(3 5) тогда
2(x-6)>0
x>6 решений нет
2 основание больше 1
x∈(-∞ 3) U (5 +∞)
2(x-6) < 0
x<6 решение x∈(-∞ 3) U ( 5 6)
Jответ x∈(-∞ 3) U ( 5 6)
Объяснение:
ну, в примере под а), у нас в числителе квадратное уравнение
и для начала, ОДЗ. думаю знаете, что на ноль делить нельзя, а если корень получится равным 2, то в знаменателе будет 0. поэтому x не может быть равным 2
дискриминант = 9-8=1 (b^2-4ac) (3^2-4*1*2)
х первое = (3-1)/2=1
x второе = (3+1)/2=2 - фантомный корень, такой нам не подойдет.
значит ответ:1
под б перенесем все в одну сторону
x+4-(5/x)=0 и приведем к общему знаменателю
(x^2+4x-5)/x=0 тут ОДЗ проще, просто x не равен нулю.
дискриминант 16+4*5=36=6^2
х первое = (-4-6)/2=-5
x второе (-4+6)/2=1
все корни подходят, ответ -5 и 1
под в это БИквадратное уравнение, нужно заменить x^2 на t (или любую другую переменную)
t^2-13t+36. дискриминант 169-4(36)=25=5^2
t первое = (13+5)/2 = 9
t второе = (13-5)/2=4
теперь возвращаемся к x^2. раз t=x^2=4, значит x=±2
раз t=x^2=9, значит x=±3
ответ: -2, +2, -3, +3.