
11 в любой степени кончается на 1. 19 в нечетной степени кончается на 9.
Их сумма кончается на 1+9=10, то есть на 0, а значит, делится на 5.
Осталось доказать, что это число делится на 3.
11=3*3+2; 11^2019 = (3*3+2)^2019 = 2^2019.
Здесь и дальше знак = означает "такой же остаток при делении на 3".
2^2019 = (2^3)^673 = 8^673 = 2^673 = 2^3*2^670 = 8*(2^10)^67 = 2*1024^67 =
= 2*(3*341+1)^67 = 2*1^67 = 2
Таким образом, 11^2019 имеет при делении на 3 остаток 2.
19 = 3*6+1; 19^2019 = (3*6+1)^2019 = 1^2019 = 1.
Таким образом, 19^2019 имеет при делении на 3 остаток 1.
Сумма этих чисел имеет остаток 2+1=3, то есть делится нацело.
Что и требовалось доказать.
Если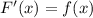 , то функция
, то функция 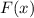 является первообразной для функции
является первообразной для функции 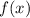 .
.