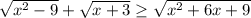(+ график, на котором представлено решение неравенства)
Теория вероятности, причем задача из простых.
Рассмотрим все карточки, у нас есть 3 буквы "А", 1 буква "Т" и одна буква "К"
Пусть мы тянем в первый раз карточку, нам нужна буква "А", а таких 3, следовательно вероятность 60% или 0.6.
Потом нам нужна буква "Т", но она одна и осталось 4 карточки => вероятность 1/4 или 0.25
Потом нам нужна снова буква "А", но их 2 осталось и 3 карточки => вероятность 2/3
Потом нам нужна буква "К", но она одна и осталось 2 карточки => вероятность 1/2 или 0.5
Осталась одна карточка и одна буква => вероятность 100% или 1
Потом все значения перемножаем
0.6* 0.25 * 2/3 * 0.5 * 1= 0.05
x(x+12)>0;
Нули неравенства:
x=-12 или x=0.
Ветви параболы направлены вверх, значит решением являются промежутки:
(-∞;-12)∪(0;+∞).
2) 2x²-3x<0;
x(2x-3)<0;
Нули неравенства:
х=0 или 2х-3=0;
2х=3;
х=1,5.
Ветви параболы направлены вверх, значит решением является промежуток:
(0;1,5).
3) x²-7x-18>0;
Находим нули неравенства:
D=49+72=121;
x1=(7-11)/2=-4/2=-2;
x2=(7+11)/2=18/2=9.
Ветви параболы направлены вверх, значит решением являются промежутки:
(-∞;-2)∪(9;+∞).
4) x²-14x>0;
x(x-14)>0;
Нули неравенства:
х=0 или х=14.
Ветви параболы направлены вверх, значит решением являются промежутки:
(-∞;0)∪(14;+∞).
5) 3x²+5x<0;
х(3х+5)<0;
Нули неравенства:
3х+5=0 или х=0;
3х=-5
х=-5/3.
Ветви параболы направлены вверх, значит решением является промежуток:
(-5/3;0).
6) x²-5x-24<0;
Находим нули неравенства:
D=25+96=121;
x1=(5-11)/2=-6/2=-3;
x2=(5+11)/2=16/2=8.
Ветви параболы направлены вверх, значит решением является промежуток:
(-3;8).