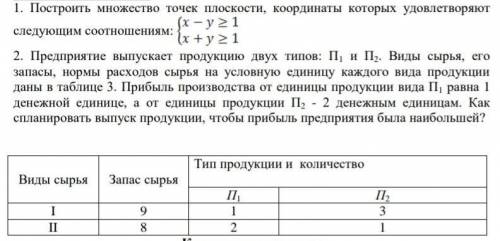
Масса одного яблока 120 г, масса олной груши 110 г
Объяснение:
Исправим условие задачи: ; кг яблок и 3 кг груш не может быть равно 810 г Поэтому читаем условие так: 4 яблока и 3 груши имеют массу 810 г.
Пусть х - масса 1-го яблока
у - масса одной груши
4/х - количество яблок
По условию
4х + 3у = 810 (1)
3х - 2у = 140 (2)
Умножаем 1-е уравнение на 3, а 2-е уравнение на -4
12х + 9у = 2430
-12х + 8у = -560
Сложим эти уравнения
17у = 1870
у = 110 (г) - масса 1-й груши
Подставим х = 110 в 1-е уравнение
4х + 3 · 110 = 810
4х + 330 = 810
4х = 480
х = 120 (г) - масса 1-го яблока
1)(4;2)
2)(2;4)
Объяснение:
⇒у=6-х; 8у+2х=3ху; 8(6-х)+2х=3х(6-х); 48-8х+2х-18х+3х²=0; 3х²-24х+48=0; х²-8х+16=0; Д=0; х=4; у=6-х=6-4=2; ответ: (4;2)
Сложим первое и второе уравнения, получим
2x=8
x=4
Тогда, выразив из первого уравнения y: y=6-x=6-4=2
2)пусть х=у-2.подставим это значение в уравнение у-2х=0 и решим его :
у-2(у-2)=0
у-2у+4=0
-у+4=0
-у=-4
у=4
Подставим полученное значение у в уравнение : у-х=2, 4-х=2 .
Решив, получаем значение х= 2.Для проверки подставляем полученные зн-я х=2 и у=4 в исходные уравнения
Наибольшая прибыль = 7 денежных единиц
Объяснение:
Пусть x - количество произведенной продукции П1, а y - количество произведенной продукции П2. Тогда цель задачи максимизировать значение (
) при условии ограничений на сырье и того, что нам надо произвести хоть что-то: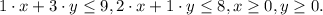 
Эти четыре неравенства задают заштрихованный под прямыми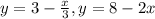
четырехугольник в первом квадранте.
Значение максимизируемого выражения x+2y есть линии уровня z=x+2y, а так как градиент функции z(x,y) равный grad z = {1;2} направлен в сторону первого квадранта, то значения z будут тем больше, чем дальше мы продвинем линию уровня в первый квадрант. С учетом ограничений наибольшее значение изготовленной продукции придется на пересечение прямых, которые задают четырехугольник: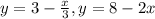
. Точка пересечения (3;2). Значит, наибольшая прибыль, которую можно получить 3+2*2=7.