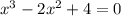
5(3-5a)²-5(3a-7)(3a+7)=5(9-30а+25а²)-5(9а²-49)=45-150а+125а²-45а²+245=
(125а²-45а²)-150а+(45+245)=80а²-150а+290
(а+1)²+3(а-1)²-5(а+1)(а-1)=а²+2а+1+3(а²-2а+1)-5(а²-1)=а²+2а+1+3а²-6а+3-5а²+5=
(а²+3а²-5а²)+(2а-6а)+(1+3+5)=-а²-4а+9
(m-1)²-4(m+1)²-6(m+1)(m-1)=m²-2m+1-4(m²+2m+1)-6(m²-1)=m²-2m+1-4m²-8m-4-6m²+6=(m²-4m²-6m²)+(-2m-8m)+(1-4+6)=-9m²-10m+3
5(1-y)²-(3+y)²-3(1-y)(1+y)=5(1-2y+y²)-(9+6y+y²)-3(1-y²)=5-10y+5y²-9-6y-y²-3+3y²=
(5y²-y²+3y²)+(-10y-6y)+(5-9-3)=7y²-16y-7
5(1+m)(1-m)-(2-m)²-8(1-m)²=5(1-m²)-(4-4m+m²)-8(1-2m+m²)=5-5m²-4+4m-m²-8+16m-8m²=(-5m²-m²-8m²)+(4m+16m)+(5-4-8)=-14m²+20m-7
а)
8x^2-4x-x^2+9
7x^2-4x+9
b)(р+3)(р-11)+(р+6)²
p^2 -8p-33+ p^2+12p+36 = 2p^2+4p+3
в)7(а+b)²-14 ab
7a^2+14ab+7b^2-14ab=7a^2+7b^2
2. Разложите на множители:
а) γ³-49γ ; б) -3а²-6ab-3b²
a)y(y^2-49)=y(y-7)(y+7)
б) -3а²-6ab-3b² =-(3a^2+6ab +3b^2)=-3(a+b)^2
3. Упростите выражение:
(а-1)²(а+1)+(а+1)(а-1) и найдите его значение при а= -3
16*-2+8=-32+8 =-24
а) (γ-6)²-(3γ)² = (y-6-3y)(y-6+3y)
б) с²-d²-c-d =(c-d)(c+d) - (c+d)=(c+d)(c-d-1)
(х-γ)² + (х+γ)²=2(х²+γ²)
x^2-2xy+y^2+x^2+2xy+y^2=2(x^2+y^ 2)
2x^2+2y^2=2 (x^2+y^2)
Объяснение:
Найдем дискриминант кубического уравнения:
У нас:
Теперь это нужно посчитать:
Поскольку D<0, то уравнение имеет 1 вещественный корень.
Выделим полный куб из выражения.
Предварительно вспомним, что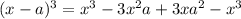 .
.
У нас:
Тогда, учитывая, что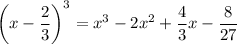 , получим:
, получим:
А теперь вынесем 4/3 за скобки:
Теперь можно делать замену вида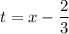 .
.
Получим:
Мы привели уравнение к виду, где отсутствует член со 2-ой степенью неизвестного. Первый этап выполнен.
Второй этап будет заключаться в сведении полученного уравнения к квадратному.
Выполним новую замену:
Тогда получим:
Посчитав это получим:
Решив это уравнение через дискриминант получим:
Берем один любой q.
Я возьму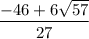 .
.
Выполним обратную замену:
Выполним вторую обратную замену:
Уравнение решено!