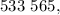 которая должна выражать дату (в каком-то неизвестном представлении).
которая должна выражать дату (в каком-то неизвестном представлении).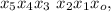


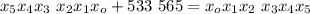 ;
;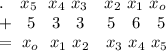

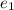 – возможная добавочная единица, уходящая из первого
– возможная добавочная единица, уходящая из первого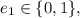
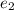 – возможная добавочная единица, уходящая из второго
– возможная добавочная единица, уходящая из второго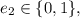
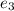 – возможная добавочная единица,
– возможная добавочная единица,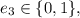
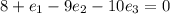 ;
;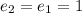 и при
и при  ;
;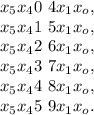
 поскольку
поскольку 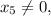 так как с этой цифры начинается разностное число.
так как с этой цифры начинается разностное число. поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.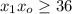 .
.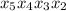 .
.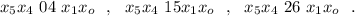
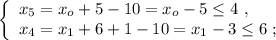

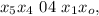
 может играть роль апреля.
может играть роль апреля.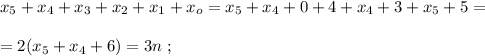
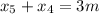 ;
;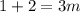 ;
;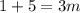 ;
;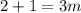 ;
; ;
;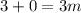 ;
;
 – дата 12/04/56 г.
– дата 12/04/56 г. – дата 15/04/86 г.
– дата 15/04/86 г.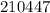 – дата 21/04/47 г.
– дата 21/04/47 г.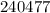 – дата 24/04/77 г.
– дата 24/04/77 г.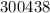 – дата 24/04/38 г.
– дата 24/04/38 г.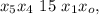
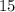 может играть только роль числа месяца (дня).
может играть только роль числа месяца (дня).
 ;
;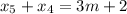 ;
;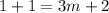 ;
;
 – дата 11/15/46 г.
– дата 11/15/46 г.

Объяснение:
Мышцы ног – самая большая мышечная группа. Составляет примерно 50% общей мускулатуры человека. Это ягодичные мышцы, квадрицепсы, бицепсы бедра, икроножные мышцы.
Мышцы живота – прямые и косые мышцы.
Для поддержания мышц в тонусе и оздоровления существуют разные комплексы упражнений. В свою очередь эти упражнения условно можно разделить на три группы:
• упражнения, в которых участвует одна группа мышц;
• упражнения, в которых участвуют несколько групп мышц;
• упражнения, в которых участвуют почти все группы мышц.
Нельзя забывать, что все упражнения нужно выполнять в определённой последовательности и дозировке. Обычно упражнения начинают делать с головы, а заканчивают прыжками, бегом или ходьбой на месте.
Дозировка нагрузки – это важный момент в выполнении упражнений, касающийся изменения интенсивности и длительности нагрузки. Упражнения можно делать дольше и интенсивнее или, наоборот, уменьшить интенсивность и количество упражнений на те или иные группы мышц при их усталости. Также это касается и интервалов между упражнениями.
Существует много разных упражнений, но составляя свой комплекс, нужно точно знать цель упражнения, его дозировку и последовательность упражнений в комплексе.
Рассмотрим разминочный комплекс из 12 упражнений.
Для мышц шеи
- и. п. ноги на ширине плеч, руки на пояс. Наклоны головой. На счёт 1 наклон головы вперёд, на счёт 2 назад, на счёт три 3 в левую сторону, на счёт 4 в правую сторону.
- и. п. тоже. Повороты головой. На счёт 1,2 поворот головы в левую сторону, на счёт 3,4 в правую сторону.
- и. п. тоже. Круговые движения головой. На счёт 1,2,3,4 круговые движения в левую сторону. На счёт 1,2,3,4 в правую сторону.
Для мышц рук
- и. п. ноги на вместе, правую руку вверх над головой, левую руку вниз в дол туловища. Рывки руками. На счёт 1,2 рывки руками, на счёт 3,4 смена положения рук.
- и. п. ноги на ширине плеч, руки перед грудью. Рывки руками. На счёт 1,2 рывки руками перед собой, на счёт 3,4 рывки руками с отведением рук в левую сторону. На счёт 1,2 рывки руками перед собой, на счёт 3,4 рывки руками с отведением рук в правую сторону.
- и. п. ноги на ширине плеч, руки к плечам. Круговые движения плечами. На счёт 1,2,3,4 круговые движения вперёд. На счёт 1,2.3,4 круговые движения назад.
Для мышц спины и ног
- и. п. ноги на ширине плеч, руки на пояс. Наклоны туловища. На счёт 1 наклон туловища вперёд, на 2 назад, на 3 в левую сторону, на 4 в правую сторону.
- и. п. тоже. Повороты туловищем. На счёт 1,2 повороты туловища в левую сторону, на счёт 3,4 в правую сторону.
- и. п. тоже. Круговые движения туловищем. На счёт 1,2,3,4 круговые движения туловищем в левую сторону, на счёт 1,2,3,4 в правую сторону.
Для мышц ног
- и. п. Ноги вместе. Руки на пояс. Прыжки на месте.
- и. п. Ноги на ширине плеч, руки вытянули перед собой. Махи ногами. На счёт 1,2 махом левой ноги носком касаемся кисти правой руки, на счёт 3,4 махом правой ноги носком касаемся кисти левой руки.
- и. п. (для девочек) руки на пояс, ноги на ширине плеч. (для мальчиков) руки за голову ноги на ширине плеч.
Приседания.