Существует решения систем уравнений: 1.Графическии подстановки сложения Самый надежный подстановки - выражаешь игрек через икс(или икс через игрек смотря что удобнее) например, было 5х+у=12, а стало у=12-5х; было 5у+х=12, а стало х=12-5у Дальше выраженный игрек или икс из одного уравнения подставляем во второе и решить уравнение с одной переменной: Х+3У=9 2Х-У=4 У=2Х-4(выразили У через Х) Подставляем 2Х-4 в первое уравнение Х+3×(2Х+4)=9 Решаем обычноу уравнение содной переменной Х+6Х-12=9 7Х=9+12 7Х=21 Х=3
Оба графика представляют линейную функцию, т.е. оба графика - прямые линии. У обоих функций одинаковый коэффициент при х, определяющий угол наклона графика к оси ОХ, следовательно оба графика - это прямые параллельные линии. При х=0 первая функция принимает значение 16, т.е. график функции пересекает ось OY в точке, где у=16. Вторая функция при х=0 принимает значение -25, т.е график функции пересекает ось OY в точке, где у=-25. Следовательно, график второй функции располагается ниже графика первой функции.
Вычислим определённый интеграл. Это и будет ответом.
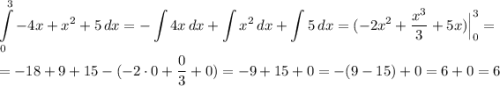
ответ: