1. а) 5xy³*(-2x²y)⁴ = 5xy³*16x⁸y⁴ = 80x¹⁺⁸y³⁺⁴ = 80x⁹y⁷
б) (2y-3x)² - (3x+2y)(2y-3x) = 4y²-12xy+9x²-6xy-9x²+4y²-6xy = 8y²-24xy
2. а) 4ab³-a³b = ab (4b²-a²) = ab (2b-a)(2b+a)
б) -9b-6b²-b³ = -b (9+6b+b²) = -b (b+3)²
3. 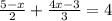
Здесь делаем всем НОЗ: 6.
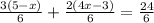
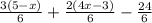
Теперь, когда у нас стали одинаковые знаменатели, решаем только числитель:
3(5-x)+2(4x-3)-24 = 0
15-3x+8x-6-24 = 0
-3x+8x+15-6-24 = 0
-5x-13 = 0
-5x = 13
x = -2,6
4. Увы, задачу не понял.
5. y = 4x-7 - линейная функция, графиком является прямая.
y = x+83 - линейная функция, графиком является прямая.
Построим таблицы:
1) y = 4x-7
x | 0 1
y | -7 -3
y₁ = 4*0-7 = -7
y₂ = 4*1-7 = -3
2) y = x+83
x | 0 1
y | 83 84
y₁ = 0+83 = 83
y₂ = 1+83 = 84
Как строить координатную плоскость - думаю, не надо объяснять.
можно смотреть и график функции тангенс, например...
я "отталкиваюсь" от известных значений
"благородных" углов (как их называл мой Учитель)...
0-30-45-60-90 градусов... и "смотрю их" на единичной окружности...
Известно:
tg 0 = 0
tg 30 = V3/3 =примерно 0.57
tg 45 = 1
tg 60 = V3 =примерно 1.7 (прямо отметьте их точками на единичной окружности)
tg 90 -> +бесконечность...
Это 1квадрант плоскости... Когда угол, увеличиваясь, становится > 90 градусов, мы попадаем во 2квадрант ---там косинус меняет знак и тангенс становится отрицательным, но значения по модулю сопоставимы с уже перечисленными значениями тангенсов...
tg (90+30) = -tg 60 =примерно -1.7
tg (90+45) = -tg 45 = -1
и т.д Нас интересует угол, тангенс которого = -5 (arctg (-5))
очевидно, что этот угол будет ближе к 90 градусам, чем угол (90+30) = (120), т.е. угол будет меньше 120 градусов...
arctg (-5) угол от 90 до 120 градусов... обычно такой оценки хватает для отбора...
аналогично про arccos(1/3)
cos 0 = 1
cos 30 = V3/2 =примерно 0.85
cos 45 = V2/2 =примерно 0.7
cos 60 = 1/2 = 0.5
cos 90 = 0
1/3 =примерно 0.33 ---это между (0 и 0.5) => угол между (90 и 60) градусов...
а (Pi - arccos1/3) диапазон от (180-90=90) до (180-60=120) => угол между (90 и 120) градусов...