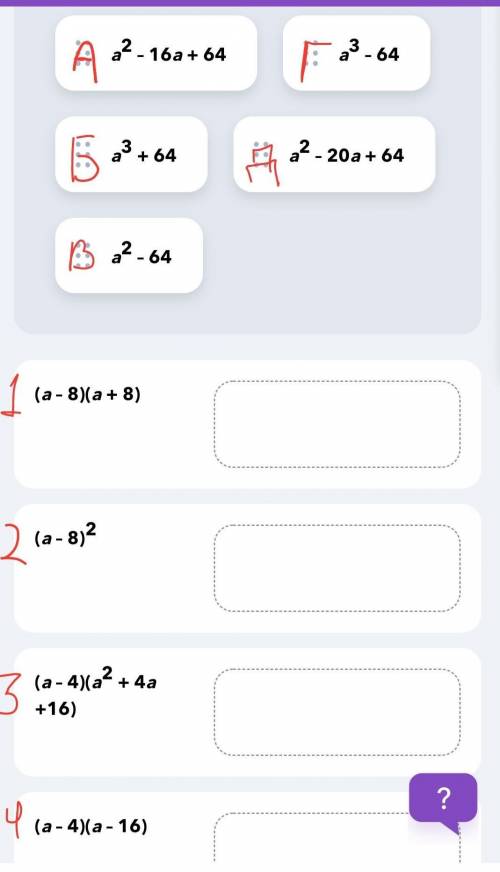
А) (а²-16а+64)=(а-8)² это 2)
Б)а³+64=(а+4)(а²- 4а+ 16) ответа не нашел в предложенных
В) а²-64=(а-8)(а+8) это 1)
Г) а³-64=(а-4)(а²+ 4а+ 16) это 3)
Д) а²-20а+64 =(а-4)(а-16) это 4)
7,5 см
Объяснение:
Розглянемо трикутники АВС і АКМ. У них:
1. Кут А -загальний.
2. Кут АКМ = кутку АВС, так як пряма КМ паралельна прямий ВС, і ці кути є відповідними.
Значить, трикутники АКМ а АВС подібні по двох кутах.
Подібні трикутники-це трикутники, у яких всі три кути рівні, а всі сторони одного трикутника в один і той же число разів довше (або коротше) сторін іншого трикутника.
Сторона АВ = АК + КМ, 6+2=8 см.
Подібна сторона АК до АВ = 6/8 или 3/4 - це коефіцієнт подібності.
Тепер дізнаємося довжину сторони КМ, вона дорівнює х/10.
Вирішимо пропорцію:
Подобно звёздам на небосводе сияют в числовом космосе простые числа. Не одну тысячу лет к ним приковано внимание математиков – их вновь и вновь ищут, исследуют, находят им применение. Евклид и Эратосфен, Эйлер и Гаусс, Рамануджан и Харди, Чебышёв и Виноградов... Этот перечень выдающихся учёных занимавшихся простыми числами и задачами с ними связанными можно продолжать и продолжать.
На страницах нашего сайта уже шла речь о бесконечности ряда простых чисел и некоторых смежных вопросах. При этом нас интересовали все простые числа сразу. Иногда же интересно рассмотреть совокупности из двух, трёх, четырёх или более простых чисел. Именно о таких совокупностях – созвездиях простых чисел – пойдёт речь далее.
Простые числа-близнецыДва простых числа, которые отличаются на 2, как
5 и 7,
11 и 13,
17 и 19,
получили образное название близнецы (эти числа называют ещё парными простыми числами). Любопытно, что в натуральном ряду имеется даже тройня простых чисел – это числа
3, 5, 7.
Ну а сколько всего существует близнецов – современной математике неизвестно.
Числа-близнецы из заданной таблицы чисел можно просеивать, слегка подправив решето Эратосфена. Если для каждого вычеркнутого Эратосфена числа n вычеркнуть так же число n – 2, то в таблице останутся лишь такие числа р, для которых число р + 2 тоже простое. В пределах первой сотни близнецы – это следующие пары чисел:
3 и 5,
5 и 7,
11 и 13,
17 и 19,
29 и 31,
41 и 43,
59 и 61,
71 и 73.
С парами близнецов в пределах 10000 можно познакомиться на страницах нашего сайта в Таблице простых и парных простых чисел, не превосходящих 10000, где они выделены красным цветом.
Вот лишь некоторые свойства этих чисел, которых лежат на самой поверхности океана простых чисел:
все пары простых близнецов, кроме 3 и 5, имеют вид 6n ± 1;при делении на 30 все пары близнецов, кроме первых двух, дают следующие пары остатков:11 и 13,
17 и 19,
29 и 1;
по мере удаления от нуля близнецов становится всё меньше и меньше. Так, в пределах первой сотни натуральных чисел существуют восемь пар близнецов, а в пределах пяти сотен с 9501 по 10000 – шесть.Предполагается, что пар простых чисел-близнецов бесконечно много, но это не доказано. Исследования, проводимые в "глубоком числовом космосе", продолжают выявлять эти замечательные и загадочные пары. На данный момент рекордсменами считаются близнецы
3756801695685 · 2666669 ± 1,
которые были обнаружены 24 декабря 2011 года в рамках реализации проекта PrimeGrid. Для записи каждого из этих чисел понадобиться 200700 цифр.
Простые числа-триплеты
Это тройка различных простых чисел, разность между наибольшим и наименьшим из которых минимальна. Наименьшими простыми числами, отвечающими заданному условию, являются –
2, 3, 5 и 3, 5, 7.
Данная пара триплетов исключительна, так как во всех остальных случаях разность между первым и третьим членом равна шести. Обобщённо: последовательность простых чисел
p, p+2, p+6 или p, p+4, p+6
называется триплетом.
Простые числа-триплеты в пределах первой сотни:
5, 7, 11;
7, 11, 13;
11, 13, 17;
13, 17, 19;
17, 19, 23;
37, 41, 43;
41, 43, 47;
67, 71, 73.
Надеюсь
Объяснение:
1)(a-8)(a+8)=a^2-64=B
2)(a-8)^2=a^2-16a+64=A
3)(a-4)(a^2+4a+16)=a^3+4a^2+16a-4a^2-16a-64=a^3-64=Г
4)(a-4)(a-16)=a^2-16a-4a+64=a^2-20a+64=Д