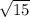sin(x)1+cos(x)+1+cos(x)sin(x)
Тригонометрия Примеры
Тригонометрия
Упростить (sin(x))/(1+cos(x))+(1+cos(x))/(sin(x))
sin(x)1+cos(x)+1+cos(x)sin(x)
Для записи sin(x)1+cos(x)
в виде дроби с общим знаменателем, умножим ее на sin(x)sin(x)
.
sin(x)1+cos(x)⋅sin(x)sin(x)+1+cos(x)sin(x)
Для записи 1+cos(x)sin(x)
в виде дроби с общим знаменателем, умножим ее на 1+cos(x)1+cos(x)
.
sin(x)1+cos(x)⋅sin(x)sin(x)+1+cos(x)sin(x)⋅1+cos(x)1+cos(x)
Запишем каждое выражение с общим знаменателем (1+cos(x))sin(x)
, умножив на подходящий множитель 1
.
sin(x)sin(x)sin(x)(1+cos(x))+(1+cos(x))(1+cos(x))sin(x)(1+cos(x))
Скомбинируем числители с общим знаменателем.
sin(x)sin(x)+(1+cos(x))(1+cos(x))sin(x)(1+cos(x))
Упростим числитель.
2(1+cos(x))sin(x)(1+cos(x))
Сократить общий множитель 1+cos(x)
.
2sin(x)
Разложим дроби.
21⋅1sin(x)
Преобразование из 1sin(x)
в csc(x)
.
21csc(x)
Делим 2
на 1
.
2csc(x)
sin(x)1+cos(x)+1+cos(x)sin(x)
Тригонометрия Примеры
Тригонометрия
Упростить (sin(x))/(1+cos(x))+(1+cos(x))/(sin(x))
sin(x)1+cos(x)+1+cos(x)sin(x)
Для записи sin(x)1+cos(x)
в виде дроби с общим знаменателем, умножим ее на sin(x)sin(x)
.
sin(x)1+cos(x)⋅sin(x)sin(x)+1+cos(x)sin(x)
Для записи 1+cos(x)sin(x)
в виде дроби с общим знаменателем, умножим ее на 1+cos(x)1+cos(x)
.
sin(x)1+cos(x)⋅sin(x)sin(x)+1+cos(x)sin(x)⋅1+cos(x)1+cos(x)
Запишем каждое выражение с общим знаменателем (1+cos(x))sin(x)
, умножив на подходящий множитель 1
.
sin(x)sin(x)sin(x)(1+cos(x))+(1+cos(x))(1+cos(x))sin(x)(1+cos(x))
Скомбинируем числители с общим знаменателем.
sin(x)sin(x)+(1+cos(x))(1+cos(x))sin(x)(1+cos(x))
Упростим числитель.
2(1+cos(x))sin(x)(1+cos(x))
Сократить общий множитель 1+cos(x)
.
2sin(x)
Разложим дроби.
21⋅1sin(x)
Преобразование из 1sin(x)
в csc(x)
.
21csc(x)
Делим 2
на 1
.
2csc(x)
1)4x²-3x-1=0
D=9+16=25=5²
X1=(3-5)/8=-2/8=-1/4
X2=(3+5)/8=1
2)6x²+7x-5=0
D=49+120=169=13²
X1=(-7-13)/12=-20/12=-5/3
X2=(-7+13)/12=6/12=1/2
3)x²-3x+2=0
D=9-8=1
X1=(3-1)/2=2/2=1
X2=(3+1)/2=4/2=2
4)(x-6)²-2x(x+3)=30-12x
x²-12x+36-2x²-6x-30+12x=0
-x²-6x+6=0
D=36+24=60=(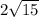 ) ²
) ²
X1=(6-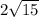 )/-2=
)/-2=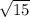 -3
-3
X2=(6+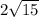 )/-2=-3-
)/-2=-3-