
Кол-во таких чисел=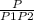 .
.
Здесь P -общее кол0во перестановок 6 чисел : P=6!=60*12
P1 - число перестановок цифры 1 в этом числе. То есть мы как бы путем деления общего числа перестановок на число перестановк конкретной цифры убираем повторяющиеся перестановки, образуемые этой цифрой. Так как кол-во единиц в наборе 2 штуки, то
P1=2!=2
Аналогично для P2=3!=6
P= 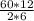 =60.
=60.
если бы например в наборе были бы только единицы напрмиер, то получилось бы единственное возможное число, что доказывает некоторую универсальность моей формулой
Объединим две книги по математике в одну условную, грубо говоря склеим их. Тогда у нас получится 4 книги (3 по физике + 1 по математике). Их расставить на полке можно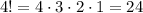
Теперь для каждого расстановки мы можем переставлять внутри одной условной книги по математике две реальные книги произвольным образом. Это можно сделать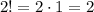
Таким образом, общее число сделать нужную расстановку существует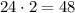 .
.
ответ: 48