Question

Очень
Подробное и понятное решение

НАЙДИТЕ ОБЛАСТИ ОПРЕДЕЛЕНИЯ ФУНКЦИЙ.
​

Answer 1

$1)\ \ y=\dfrac{\sqrt{1+x}}{x^2-3x-10}\ \ ,\ \ \ OOF:\ \left\{\begin{array}{l}11+x\geq 0\\x^2-3x-10\ne 0\end{array}\right\\\\\\\left\{\begin{array}{l}x\geq -11\\(x+2)(x-5)\ne 0\end{array}\right\ \ \left\{\begin{array}{l}x\geq -11\\x\ne -2\ ,\ x\ne 5\end{array}\right\\\\\\x\in [-11\, ;-2\, )\cup (-2\, ;\, 5\, )\cup (\, 5\, ;+\infty \, )$

$2)\ \ y=\dfrac{\sqrt{4-8x}}{\sqrt{x^2-4,5x-9}}\ \ ,\ \ \ \ OOF:\ \ \left\{\begin{array}{l}4-8x\geq 0\\x^2-4,5x-90\end{array}\right\\\\\\\left\{\begin{array}{l}8x\leq 4\\(x+1,5)(x-6)0\end{array}\right\ \ \ \left\{\begin{array}{l}x\leq 0,5\\x\in (-\infty ;\, -1,5\, )\cup (\ 6\, ;+\infty )\end{array}\right\\\\\\x\in (-\infty \, ;\, -1,5\, )$

Answer 2

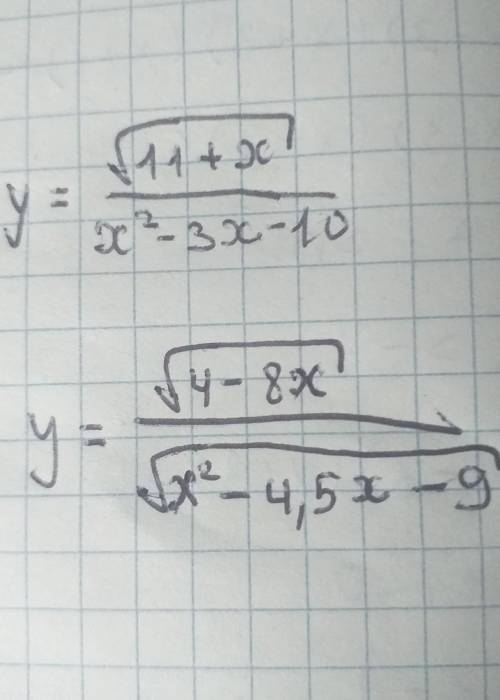
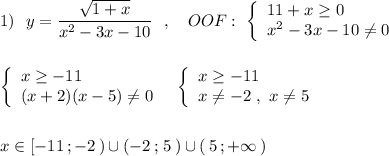
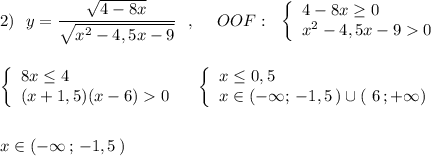
1. корень четной степени существует. если подкоренное выражение неотрицательно. т.е. 11+х≥0, х≥-11, на нуль делить нельзя, поэтому х²-3х-10≠0; по Виету корнями уравнения х²-3х-10=0 служат х=5;х=-2, тогда ОДЗ х≠5, х≠-2, окончательно, D(у)=[-11; -2)∪(-2;5)∪(5;+∞)

2. 4-8х≥0; х≤0.5; х²-4.5х-9>0; решим уравнение  х²-4.5х-9=0;

х=(4.5±√(20.25+36)/2=(4.5±√(56.25)/2=(4.5±7.5)/2; х=6; х=-1.5, вернемся к последнему неравенству.

-1.56

  +                     -                 +

х∈(-∞;-1.5)∪(6;+∞)

Областью определения будет пересечение двух решений неравенств.

х∈(-∞;-1.5)