
а) 3 у=-2х+2
угол наклона к положительному направлению оси ох тупой. ордината точки пересечения с осью оу равна 2
б) 1) , у =2х+2 угол наклона к положительному направлению оси ох острый. ордината точки пересечения с осью оу равна 2
в) 2) у=-2х-2 угол наклона к положительному направлению оси ох тупой. ордината точки пересечения с осью оу равна -2
х км/ч скорость катера
(х + 1,5) км/ч скорость катера по течению
(х - 1,5) км/ч скорость катера против течения
2(х+1,5) км катер по течению реки за 2 часа
3(х-1,5) км катер против течения реки за 3 часа
По условию известно, что за 2 часа катер проходит по течению реки в 1.25 раза меньше ,чем за 3 часа против течения реки.
Получаем уравнение:
1,25 * 2(х+1,5) = 3(х-1,5)
2,5(х+1,5) = 3х - 4,5
2,5х + 3,75 = 3х - 4,5
3х - 2,5х = 8,25
0,5х = 8,25
х = 8,25 6 0,5
х = 16,5
ответ. 16,% км/ч скорость катера в стоячей воде
2x - y = -3; <=> y = 2x + 3. (1)
3x + y = -2; <=> y = -3x - 2. (2)
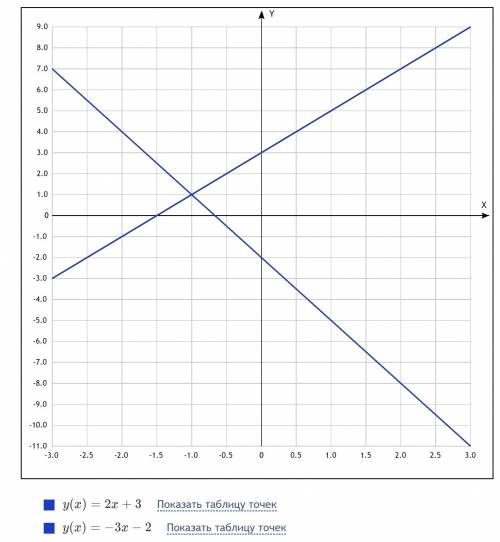
Построим графики функций (1) и (2). Координаты точки их пересечения и будут решением системы.
Функции (1) и (2) линейные, то есть их графиками являются прямые. Для построения прямой достаточно двух точек.
Строим график функции (1): при x = 0 y = 3; при x = 1 y = 5. Через точки (0, 3) и (1, 5) проводим прямую.
Строим график функции (2): при x = 0 y = -2; при x = -1 y = 1. Через точки (0, -2) и (-1, 1) проводим прямую.
По чертежу очевидно, что графики функций (1) и (2) пересекаются в точке (-1, 1). Следовательно, (-1, 1) - решение системы.
ответ: (-1, 1).
Чертеж:
ответ: а - 3 , б - 1 , в - 2
Объяснение:
k>0 - острый угол между прямой и полож. направлении оси ОХ
k<0 - тупой угол между прямой и полож. направлении оси ОХ
b>0 - точка пересечения прямой и оси ОУ выше оси ОХ
b<0 - точка пересечения прямой и оси ОУ ниже оси ОХ