y = 4x - x² - Квадратичная функция, график - парабола, ветви направлены вниз ( a = -1). Максимальное значение принимает в вершине, минимальное значение не имеет, снизу не ограничена.
a) Координаты вершины параболы
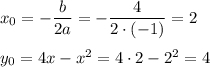
x₀=2 ∈ [0; 3] ⇒ x₀=2 - точка максимума функции попадает в заданный интервал, наибольшее значение функции y₀ = 4.
Значения функции на границах интервала
x = 0; y = 4·0 - 0² = 0
x = 3; y = 4·3 - 3² = 3
Наименьшее значение y = 0 при x = 0.
б) x∈(-∞; 2] - функция возрастает
x∈[2; +∞) - функция убывает
в) 4x - x² < 0 ⇔ x (4 - x) < 0
Метод интервалов : x₁ = 0; x₂ = 4
------------ (0) +++++++++ (4) -----------> x
x∈(-∞; 0) ∪ (4; +∞)
Первый совет по решению таких задач - делать чертёж. Без него редко что видно.
Нарисуйте это и постройте два треугольника.
1-ый треугольник - образующая большого конуса, высота большого конуса и радиус большого конуса и высота большого конуса.
2-ой треугольник - образующая маленького конуса, высота маленького конуса и радиус маленького конуса.
Эти два треугольника подобны (если не ясно почему, в лс спросите). Поскольку по условию высота меньше в 2 раза, то и все остальные стороны меньше в 2 раза - коэффициент подобия k=2.
Выражаем обьём маленького конуса через параметры большого.
1/3 * (1/2r)²π * h/2 = 1/3* 1/4r²π * 1/2 h= 1/8 (1/3r²π*h)
Обьем большого
1/3 * r²π *h
Теперь видим, что маленький в 8 раз меньше большого.Значит его объём 32/8 = 4
-179
Объяснение:
Потомушто так правильно