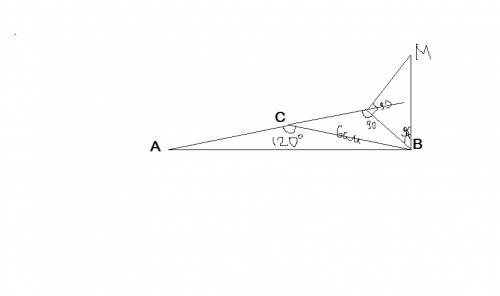
Смотри на рисунке показано что проекция выходит за пределы треугольника, так как расстояни от точки до прямой есть перпендикуляр проведенный из данной точки к данной прямой. Далее смотрим, у нас полчился треугольник ВС и допустим М(ВСМ). В нем 1. угол равен 90 градусов, воторой 60( смежный с 120) и третий следовательно 30 градусов. В прямоугольном треугольнике катет лежащий напротив угла в 30 градусов равен половине гипотенузы. слеовательно равен 3. Далее по теореме пифагора проекция наклонной получается равна 5. и по той же теореме пифагора наша искомая наклонная равна 6.
Каноническое уравнение, задающее эллипс, выглядит так:
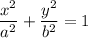
Перепишем уравнение эллипса, поменяв местами параметры  и
и 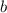 :
:
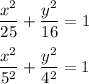
При этом мы получим конгруэнтный эллипс, только повёрнутый в системе координат на 90° (конгруэнтность следует из симметричности канонического уравнения). Поэтому он будет иметь тот же эксцентриситет и то же фокальное расстояние.
Найдём эксцентриситет:
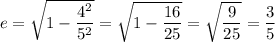
Найдём фокальное расстояние (полурасстояние между фокусами):
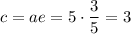
Тогда расстояние между фокусами в два раза больше: 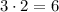 .
.
ответ: 6 ед.
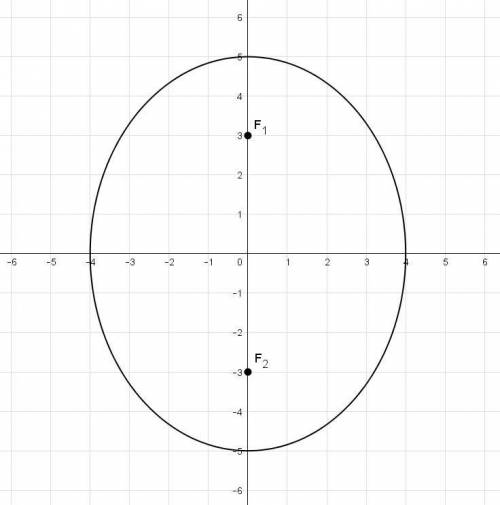
На чертеже изображён данный эллипс.  и
и 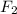 — его фокусы.
— его фокусы.
 " />
" />
Пройдя в обе стороны, туристы ровно 14 км шли наверх и 14 км шли вниз. Если скорость вверх обозначить буквой x, то общее время вычисляется как
и по условию оно равно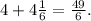 Итак,
Итак,
x=3 или x= - 4/7. Но x>0, поэтому x=3 (это скорость вверх), x+1=4 (это скорость вниз).
ответ: 3 км/час и 4км/час
Замечание. Для получения ответа нам понадобилось только общее время в пути. Вот если бы еще надо было узнать, какая часть пути идет наверх и какая вниз, тогда понадобились бы все данные. На всякий случай ответим и на этот вопрос. Если обозначить путь наверх (скажем, при движении от А до Б) буквой y, то путь вниз равен 14-y, а время движения от А до Б вычислялось бы по формуле
Таким образом, при движении от А до Б приходится 6 км идти наверх и 14-6=8км идти вниз (соответственно в обратную сторону приходится 8 км идти наверх и 6 км идти вниз).