√(11-5х)>х-1
Решение этого неравенства найдем, когда решим две системы и объединим их решения.
1)Система:{х-1≥0 {x≥1 {x≥1
{11-5х>(x-1)² {x²3x-10<0 {-5<x<2 1≤x<2
2)Система: {x-1<0 {x<1
{11-5x≥0 {x≤11/5 x<1
Объединением этих результатов(1≤х<2 и х<1) будет интервал х<2, то есть х∈(-∞,2).
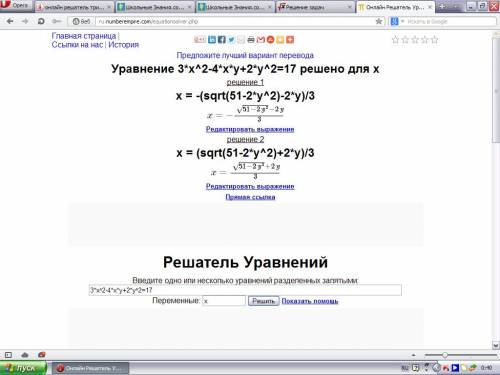
Сложим оба уравнения, получим: 4x²-4xy+y²=1 ⇒ (2x-y)²=1 ⇒2x-y=+1 или 2x-y=-1
Получим две системы {y=2x-1 или {y=2x+1
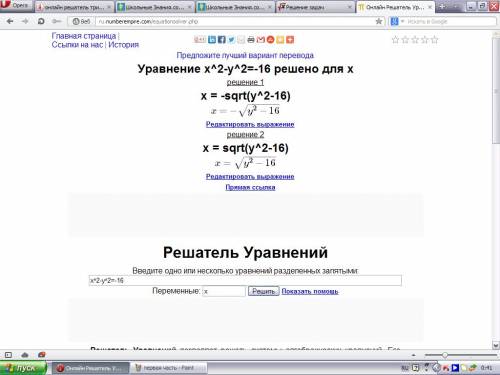
{x²-(2x-1)²=-16 {x²-(2x+1)²=-16
1) {y=2x-1 или 2) {y=2x+1
{3x²-4x-15=0 {3x²+4x-15=0
x₁=3, y₁= 6-1=5 x₁=-3 y₁=-5
x₂=-5/3, y₂=-10/3-1=-13/3 x₂=5/3 y₂=13/3
ответ: (3;5), (-5/3; -13/3), (-3;-5), (5/3; 13/3).
Число размещений из n элементов по 4 равно: A⁴n = n!/(n-4)!
Число размещений из n-2 элементов по 3 равно: A³n-2 = (n-2)!/(n-2 -3)! = (n-2)!/(n-5)!
A⁴n в 14 раз больше A ³n-2 => A⁴n : A³n-2 = 14
n!/(n-4)! : (n-2)!/(n-5)! = 14
n! * (n-5)! /(n-2)! *(n-4)! = 14
n! * 1*2*3*...*(n-5) / (n-2)! *1*2*3*...*(n-5)*(n-4) = 14 (сокращаем дробь на 1*2*3*...*(n-5) )
n! / (n-2)! *(n-4) = 14
1*2*3*..*(n-2)*(n-1)*n / 1*2*3*..*(n-2) *(n-4) = 14 (сокращаем дробь на 1*2*3*...*(n-2) )
(n-1)*n / (n-4) = 14 | *(n-4)
(n-1)*n = 14(n-4)
n² - n = 14 n - 56
n² - n - 14 n + 56 = 0
n² - 15 n + 56 = 0
D = 225 - 4*56 = 225 - 224 = 1
n₁= (15 + 1)/2 или n₂= (15 - 1)/2
n₁= 8 или n₂= 7
ответ: 7 ; 8.