нули функции это те значения аргумента функиии х, при которых ззначение функции y равно 0.
т.е. нужно найти х для которых ax^2+c=0 т.е. решить уравнение
ax^2+c=0
ax^2=-c
при а=0 и с=0 уравнение имеет вид
0x^2=0 и уравнение имеет бесконечно много нулей (функция имеет вид y=0)
если а=0 и с не равно 0 тогда решений нет (у функции нет нулей)
если а не равно 0, тогда перепишем уравнение в виде
x^2=-c/a которое имеет решение при условии -c/a>=0
т.е. при (a>0, c<=0 или a<0, c>=0)
итого данная функция имеет нули при a>0, c<=0
или a<0, c>=0
или а=с=0
Объяснение:
Подставим координаты точки в каждое уравнение системы . Если получим верные числовые равенства, то данная пара является решением системы .
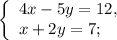
(-3;2) 4*(-3) -5*2 =12;
-12-10=12;
-22≠ 12
Подставлять во второе уравнение не имеет смысла
(-3;2) - не является решением системы.
(3; -2) 4*3-5*(-2)=12
12+10=12
22≠12
(3;-2) - не является решением системы.
(3;2) 4*3-5*2=12
12-10=12
2≠12
(3;2) - не является решением системы.
ответ: ни одна из данных пар чисел не является решением системы
Решим систему:
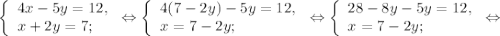
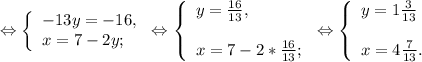
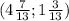 - решение данной системы. Значит ни одна из пар чисел не является решением системы.
- решение данной системы. Значит ни одна из пар чисел не является решением системы.
Могло содержаться серебра 40 гр или 180 гр.
Объяснение:
на снимке