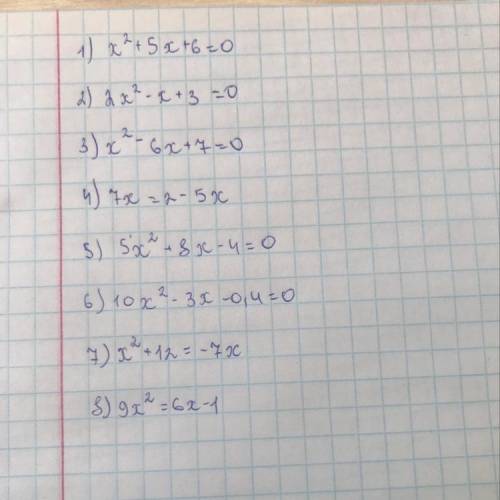
В решении.
Объяснение:
Построить графики функций:
y=x
y=x+2
y=x-2
y=-x+1
y=-x-1
y=-3x+3
y=-3x
y=-3x-3.
Графики линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
1) y=x
Таблица:
х -1 0 1
у -1 0 1
2) y=x+2
Таблица:
х -1 0 1
у 1 2 3
3) y=x-2
Таблица:
х 0 1 2
у -2 -1 0
4) y= -x+1
Таблица:
х -1 0 1
у 2 1 0
5) y= -x-1
Таблица:
х -1 0 1
у 0 -1 -2
6) y= -3x+3
Таблица:
х 0 1 2
у 3 0 -3
7) y= -3x
Таблица:
х -1 0 1
у 3 0 -3
8) y= -3x-3
Таблица:
х -1 0 1
у 0 -3 -6
Графики у= -3х; у= -3х+3; у= -3х-3 параллельны (коэффициент при х одинаковый);
Графики у= х; у= х+2; у= х-2 параллельны (коэффициент при х одинаковый);
Графики у= -х+1; у= -х-1 параллельны (коэффициент при х одинаковый).

Даны точки А(2;3;-1) и прямая (х-5)/3=у/2=(z+25)/-2.
Из уравнения прямой получим: s = 3; 2; -2 это направляющий вектор прямой;
M1 = 5; 0; -25 это точка, лежащая на прямой.
Тогда вектор M0M1 = {M1x - M0x; M1y - M0y; M1z - M0z} =
= (5 - 2; 0 - 3; -25 - (-1)) = (3; -3; -24).
Площадь параллелограмма лежащего на двух векторах M0M1 и s:
S = |M0M1 × s|
M0M1 × s =
i j k
3 -3 -24
3 2 -2
= i(-3·(-2) - (-24)·2) - j(3·(-2) - (-24)·3) + k(3·2 - (-3)·3) =
= i(6 + 48) - j(-6 + 72) + k(6 + 9) = 54; -66; 15.
Зная площадь параллелограмма и длину стороны найдем высоту (расстояние от точки до прямой):
d = |M0M1×s|
|s|
= √(54² + (-66)² + 15²)
√(3² + 2² + (-2)²) =
= √7497
√17
= √441 = 21.
Объяснение:
Квадратные уравнения все можно решить с дискриминанта.
D = b^2 - 4ac
x1 = -b + sqrt(D) / 2a
x2 = -b - sqrt(D) / 2a
1. x^2 + 5x + 6
D = 25 - 24 = 1
x1 = -5 + 1 / 2 = -2
x2 = -5 - 1 / 2 = -3
2. 2x^2 - x + 3 = 0
D = 1 - 104 = -103
Отрицательный дискриминант значит что корень уравнения невычислим.
3. x^2 - 6x + 7 = 0
D = 36 - 49 = - 13.
Отрицательный дискриминант значит что корень уравнения невычислим. Проверь, там случайно не x^2 - 6x -- 7 = 0?
4. 7x = 2 - 5x
7x + 5x = 2
12x = 2
x = 2/12 = 1/6
Тут точно нет квадрата?
5. 5x^2 + 8x - 4 = 0
D = 64 + 80 = 144
x1 = -8 + 12 / 10 = 4/10 = 0,4
x2 = -8 - 12 / 10 = -2
6. 10x^2 - 3x - 0,4 = 0
D = 9 + 16 = 25
x1 = 3 + 5 / 20 = 8/20 = 0,4
x2 = 3 - 5 / 20 = -2/20 = -0,1
7. x^2 + 12 = -7x
x^2 + 7x + 12 = 0
D = 49 - 48 = 1
x1 = -7 + 1 / 2 = -3
x2 = -7 - 1 / 2 = -4
8. 9x^2 = 6x - 1
9x^2 - 6x + 1 = 0
D = 36 - 36 = 0
Дискриминант равен нулю, значит ответ только один.
x1,2 = 6 / 18 = 1/3