Уравнение касательной в определенной точке: y = f(x0) + f'(x0)(x-x0)
y = 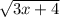
x0 = 4
f'(x) = 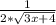 *(3x+4)' =
*(3x+4)' = 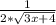 *3
*3
f'(x0) = 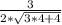 =
= 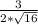 =
= 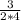 =
= 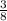
f(x0) = 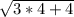 = 4
= 4
y = 4 + 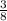 *(x-4)= 4 +
*(x-4)= 4 + 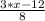 = 4 - 1.5 +
= 4 - 1.5 + 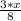 = 0.375*x + 2.5
= 0.375*x + 2.5
1) x ∈ (-∞; -8) U (3; +∞)
2) x ∈ (-∞; -3) U (5; 7)
Объяснение:
1) x^2 + 5x - 24>0
x^2 + 5x - 24=0
D= √(b^2 - 4ac) = √(5^2 - 4 * 1 * (-24)) = √(25 + 96) = √121 = 11
x = (-b +/- √D)/2a
x1 = -5 + 11 / 2 =3
x2 = -5-11 /2 = -8
Получается три интервала:
x<-8
-8<x<3
x>3
чередуем знаки справа налево, первый - плюс (так как нам нужно больше, то выбираем там, где плюс)
получаем x<-8 и x>3
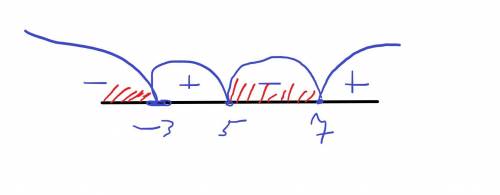
2) (x-5)(x-7)(x+3)<0
(x-5)(x-7)(x+3)=0
x = 0 тогда, когда один из множителей равен нулю:
x=5; x=7; x=-3
получаем четыре интервала (см фотку)
выбераем там, где минус, т. к. нужен знак < по условию
x<-3 и 5<x<7
y-y(4)=k(x-4) уравнение касательной
y(4)=sqrt(16)=4
k знчение производной при х=4
Производная =3/(2*sqrt(3x+4))
значение производной при х=4 будет 3/8
y-4=(3/8)*(x-4)
y=3x/8+2,5