Рассмотрим вертикальные линии и горизонтальные. Каждую из них диагональ пересекает ровно один раз. При этом каждое пересечение вертикальной или горизонтальной линии соответствует пересечению двух (соседних) клеток. Посчитаем сумму вертикальных (
) и горизонтальных клеток (
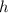): каждая клетка, которую пересекают (кроме двух крайних), считается дважды (она дважды участвует в паре), но также каждое пересечение считается дважды. Поэтому 
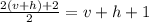есть количество пересеченных клеток (мы добавили двойку в числителе вот почему: 2(v+h) - это удвоенное количество средних клеток (т.е. не крайних), а крайние посчитаны только один раз. Добавляя 2, мы считаем и крайние два раза. Теперь все клетки посчитаны дважды — можем делить на 2)
Пусть дан прямоугольник 
, причем числа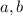 
не имеют общих делителей (иначе какая-то клетка пересекалась бы по вершине — мы ее не считали). Тогда 
, 
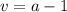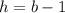. Получаем 
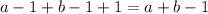пересеченная клетка. Поскольку числа 239 и 566 не имеют общих делителей, к ним применима эта формула. Получаем, что диагональ пересекает 239+566-1=804 клетки
доказать тождество1+tg2a/1-tg2a=1/cos2a-sin2a
Раскрываем скобки получается
1 - (1/cos2a) + tg2a + (1/cos2a) - (1/cos²2a) + (tg2a/cos2a) + tg2a - (tg2a/cos2a) + tg²2a=2tga
1+2tg2a - (1/cos²2a) + tg²2a=2tg2a
1 - (1/cos²2a) + tg²2a=0
((cos²2a-1) / cos²2a) + tg²2a=0
тк cos²x+sin²x=1 то
((cos²2a-cos²2a-sin²2a) / cos²2a) + tg²2a=0
- (sin²2a/cos²2a) + tg²2a=0
доказано
Объяснение: