ответ: x = 14.
Объяснение: одно дело "выразить икс" и совсем другое - решить уравнение)) можно найти икс, постепенно выполняя обратные действия (не раскрывая скобок):
1) делимое = произведению делителя и частного: 1.2*(12_2/3) = (6/5)*(38/3) = 76/5
2) слагаемое = разности суммы и другого слагаемого: (76/5)-6.2 = (76/5)-(31/5) = 45/5 = 9
3) чтобы найти делитель (это самая внутренняя скобка), нужно делимое разделить на частное:
(3_9/16):9 = (57/16)*(1/9) = (19/16)*(1/3) = 19/48
4) уменьшаемое = разность + вычитаемое: (19/48)+(7/24) = (19+14)/48 = 33/48 = 11/16
5) 2.75:(11/16) = (11/4)*(16/11) = 4
получили: х:(2/7) - 45 = 4
x:(2/7) = 45+4=49
x = 49*(2/7) = 14
и всегда полезно делать проверку:
14:(2/7) = 14*7/2 = 7*7 = 49
49-45 = 4
(2.75)/4 = (11/4)*(1/4) = 11/16
(11/16)-(7/24) = (33-14)/48 = 19/48
(3_9/16):(19/48) = (57/16)*(48/19) = 3*3 = 9
9+6.2 = 15.2
(15.2):(12_2/3) = (76/5)*(3/38) = 6/5 = 12/10 = 1.2
а выразить икс гораздо сложнее...
Найдем уравнение касательной, проходящей через точку с абсциссой
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой
:
Найдем значение производной данной функции в точке с абсциссой
:
Уравнение касательной имеет вид:
Подставим значение
Итак, уравнение касательной заданной функции: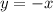
Воспользуемся геометрическим смыслом касательной: коэффициент наклона
касательной 
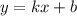численно равен тангенсу угла наклона 
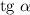с положительным направлением оси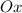 
В найденной касательной коэффициент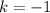
, следовательно, 
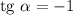при 
или 
ответ:
или 