Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 16 км/ч, а вторую половину пути проехал со скоростью 96 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 57 км/ч. ответ дайте в км/ч.
Пусть х км/ч - скорость первого автомобиля, тогда скорость, с которой второй проехал первую половину пути, равна (х-16) км/ч. Расстояние между А и В обозначим S км. Время в пути равно или часов. Составим и решим уравнение:
Пусть х см составляет один катет прямоугольного треугольника, а у см - второй катет. Гипотенуза равна: 13²=х²+у². Если один из катетов увеличить на 4 см - х+4 см, то гипотенуза увеличится на 2 см и составит 13+2=15 см. Гипотенуза равна: 15²=(х+4)²+у² Составим и решим систему уравнений (методом сложения): Умножим первое уравнение на (-1) и выполним сложение: = (-х² + (х+4)²) + (-у²+у²)= (-169)+225 (х+4)²-х²=56 х²+8х+16-х²=56 8х=56-16 8х=40 х=40:8 х=5 см - первый катет х²+у²=169 5²+у²=169 25+у²=169 у²=169-25 у²=144 у=±√144 у₁=12 у₂=-12 - не подходит, поскольку у<0 ОТВЕТ: катеты треугольника составляют 5 см и 12 см.
Условие дано с ошибкой. Правильно звучит так:
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 16 км/ч, а вторую половину пути проехал со скоростью 96 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 57 км/ч. ответ дайте в км/ч.
Пусть х км/ч - скорость первого автомобиля, тогда скорость, с которой второй проехал первую половину пути, равна (х-16) км/ч. Расстояние между А и В обозначим S км. Время в пути равно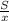 или
или 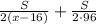 часов. Составим и решим уравнение:
часов. Составим и решим уравнение:
по теореме Виета:
ответ: скорость первого автомобиля 64 км/ч.