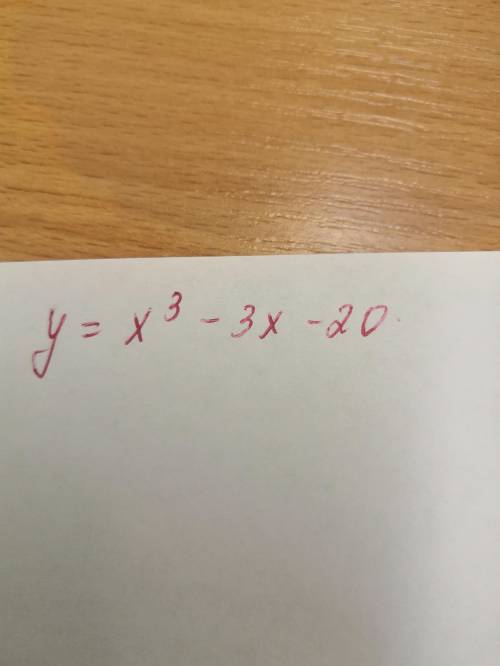
Объяснение:
y'=3x²-3
y'=0
3x²-3=0; x²-1=0;
x₁=-1;x₂=1 -точки экстремума
-1 1
+ - +
Функция возрастает на отрезках (-∞;-1) и (1;∞)
убывает (-1;1)
(-1 ;-18)- точка максимума
(1;-22) - точка минимума
№ 1
Пусть х - количество мобильных пунктов управления.
(х² - х) : 2 = 36
х² - х = 36 * 2
х² - х = 72
х² - х - 72 = 0
D = (- 1)² - 4 * (-72) = 1 + 288 = 289 = 17²
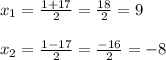
Второй корень не подходит, значит, количество мобильных пунктов управления равно 9.
ответ: 9.
№ 2
Пусть х - % снижения стоимости товара в первый раз,
тогда 2х - % снижения стоимости товара во второй раз.
(50 - 50 : 100 * х) руб. - стоимость товара после первого снижения цены;
((50 - 50 : 100 * х) - (50 - 50 : 100 * х) : 100 * 2х) руб. - стоимость товара после второго снижения цены.
(50 - 50 : 100 * х) - (50 - 50 : 100 * х) : 100 * 2х = 29,75
50 - 0,5х - (50 - 0,5х) : 100 * 2х = 29,75
50 - 0,5х - х + 0,01х² = 29,75
0,01х² - 1,5х + 50 - 29,75 = 0
0,01х² - 1,5х + 20,25 = 0
х² - 150х + 2025 = 0
D = 150² - 4 * 2025 = 22500 - 8100 = 14400 = 120²
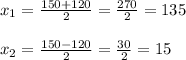
Первый корень не подходит, так как процент снижения не может быть больше 100%, значит, в первый раз цена товара снизилась на 15%.
ответ: 15%.
решение смотри на фотографии
Объяснение: