ответ и решение во вложении
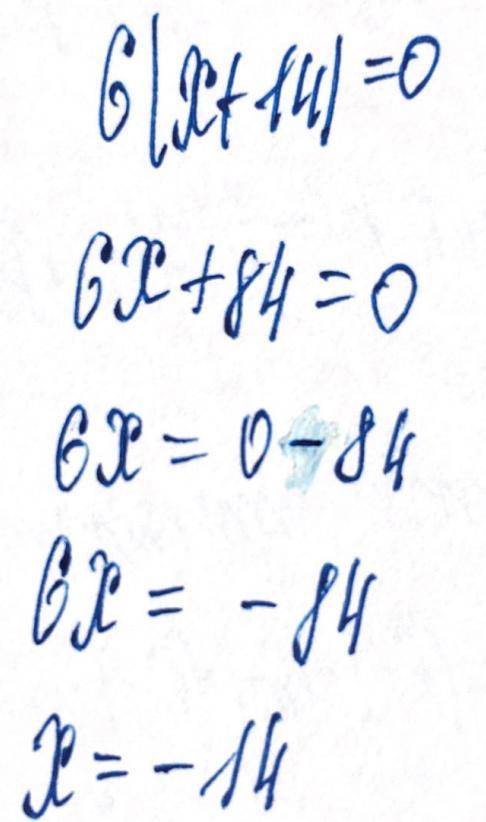
Условию удовлетворяет только одна пятерка последовательных натуральных чисел:
10; 11; 12; 13; 14
и
10²+11²+12² = 13²+14² = 365
Объяснение:
Пусть, x - первое число последовательности.
Т.к. нам нужны пять последовательных натуральных (то есть целых, неотрицательных) чисел, то они будут выглядеть так:
x; x+1; x+2; x+3; x+4
Причем x > 0
Известно, что равны:
- сумма квадратов первых трёх чисел
- сумма квадратов двух последних чисел.
т е.
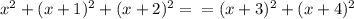
Преобразуем, раскрыв скобки:

По Т. Виетта:
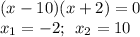
или через дискр-нт. Т.к. b четное, возьмем D/4:
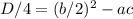
а корни будут равны
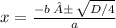
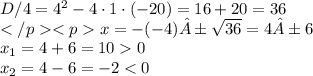
Так как в условии указано, что числа - последовательные натуральные, значение
x= -2 - не подходит, т.к. число -2 отрицательное и не является натуральным
Следовательно, первое число из пяти искомых - это 10, а вся последовательность имеет вид:
10; 11; 12; 13; 14
Проверим - и действительно:
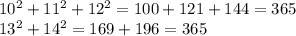
сумма квадратов первых трёх чисел равна сумме квадратов двух последних чисел.
Объяснение:
6(x+14)=0
x+14=0
x= -14