ии ипапрт импсаччсмпипавииммпмп

Какие из точек
А ( 1; 29/14 );
В ( 0; 4/7 );
С ( 1; 13/14 );
D ( -2; -17/7 );
Е ( 2/7; -1/7 )
принадлежат графику функции у = -4/7 + 1,5х
Выполним преобразования:
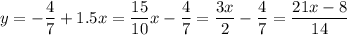
Теперь проверим наши точки
А (1; 29/14) Значит х=1; у=29/14
подставим х=1 в выражение функции
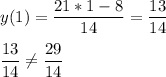
Значит точка А не принадлежит графику
В(0;4/7) Значит х=0; у=4/7
подставим:
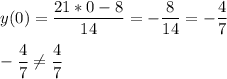
Значит точка не принадлежит графику
C(1;13/14) Значит х=1; у=13/14
Мы уже находили у(1) (см. точку А) и у(1)=13/14
Значит точка С принадлежит графику
D(-2; -17/7)
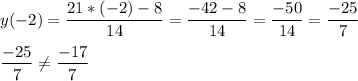
Значит точка D не принадлежит графику
E(2/7; -1/7)

Значит точка E принадлежит графику
ответ: точки С и Е принадлежать графику
Исследуйте на четность функцию :
1) y = f(x) = - 8x + x² + x³
2) y = f(x) = √(x³ + x²) - 31*| x³ |
ни четные ,ни нечетные
Объяснение:
1)
f(x) = - 8x + x² + x³ ; Область Определения Функции: D(f) = R
функция ни чётная ,ни нечётная
проверяем:
Функция является четной, когда f(x)=f(-x) , нечетной, когда f(-x)=-f(x)
а) f(-x) = - 8*(-x) +(- x)² +(- x)³ = 8x + x² - x³ ≠ f(-x)
Как видим, f(x)≠f(-x), значит функция не является четной.
б)
f(-x) ≠ - f(-x) → функция не является нечетной
- - - - - -
2)
y = f(x) = √(x³ + x²) - 31*| x³ | ,
D(f) : x³ + x² ≥ 0 ⇔ x²(x+1) ≥ 0 ⇒ x ≥ -1 * * * x ∈ [ -1 ; ∞) * * *
ООФ не симметрично относительно начало координат
* * * не определен , если x ∈ ( -∞ ; - 1) * * *
функция ни чётная ,ни нечётная
r=At A=r:t
-28(1/2+25/28)=-39