все 4 задания во вложении.
Задача номер 5.
х^2=(x-1)(x-2)+16
x^2=x^2-2x-x+2+16
x^2-x^2+2x+x=2+16
3х=18
х=18/3
х=6
ответ: 6
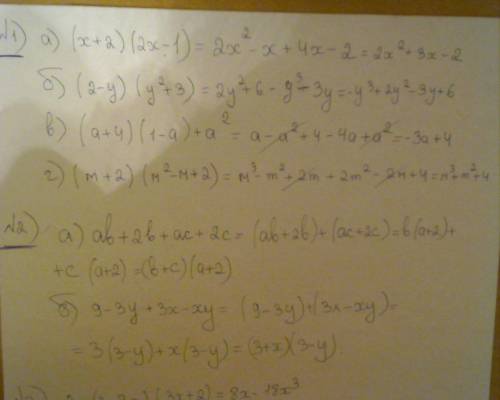
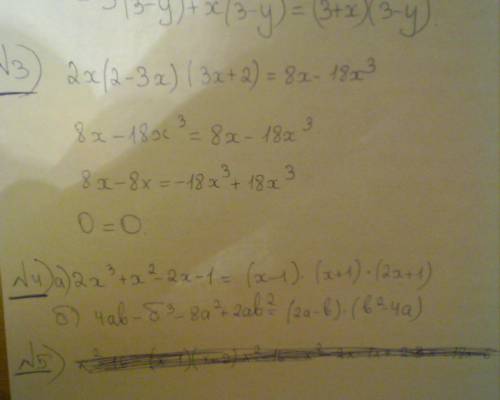
А∪В = {1, 2, 3, 4, 5, 6, 9, 11}
А∩C = {1, 6}
А\C = {2, 3, 4, 5}
А∪(В∩С) = {1, 2, 3, 4, 5, 6, 11}
(А∪В)\С = {2, 3, 4, 5, 9}
Объяснение:
А∪В - сумма множеств (элементы, которые входят в А + элементы, которые входят в В)
А∩C - умножение множеств (элементы, которые входят и в А и в В одновременно)
А\C - разница множеств (элементы множества А, которые не входят в множество С)
А∪(В∩С) - сумма множества А и множества - умножение В и С (элементы, которые входят и в А и в С одновременно + элементы множества А)
(А∪В)\С - разница множеств А+В и множества С (элементы множества А+В, которые не входят в множество С)
Объяснение:
Надо сосчитать количество входов и выходов в каждом узле. Узел-это точка в которой есть пересечения линий. если количество линий нечетное,то таких узлов не может быть больше 2. При этом начало обхода в одном нечетном узле,а окончание во втором. В данном чертеже второй рисунок имеет четыре нечетных узла.Значит вторую фигуру нельзя начертить одним росчерком карандаша.
В первом два узла по три ,это "основание перевернутого домика"
значит начинаем в одном из них и заканчиваем во стором. В третьем можно начинать в любом месте и найти как завершить обход.
а) (х+2) (2х-1)= (х+2) (1х) = х+2х= 3х