Если нужно выбрать верны утверждения, то это 2 и 4.
Смотрим, белый короче желтого, но длиннее синего.
Расположим шарфы в порядке уменьшения их длины, получаем:
Желтый, белый, синий. Читаем далее, черный не длиннее белого, следовательно, он может быть как равен по длине, так и меньше.
Тогда примерное расположение шарфов:
Желтый, белый, синий и черный(черный и синий могут меняться местами в зависимости от их длины)
Смотрим утверждение, 1 не верно, так как черный шарф может быть как равен по длине, так и меньше.
2 утверждение верно, так как читая условие делаем вывод, что желтый длиннее всех(см. выше).
3 утверждение не верно, так как в условии сказано, что белый шарф длиннее.
4 утверждение верно, так как желтый шарф самый длинный.
Объяснение:
a) По условию составляем неравенство
-2x^2 + 2x -3 > -x -1
-2x^2 + 3x -2 > 0
2x^2 - 3x + 2 < 0
x^2 - 1.5x + 1 < 0
(x^2 - 0.75)^2 + 1 < 0 - не может быть ни при каких x, потому что значение выражения (x^2 - 0.75)^2 + 1 всегда положительно, значит, f(x) не будет больше g(x) ни при каких значениях x.
б) График функции y = f(x) находится ниже графика функции y =g(x), значит, выполняется неравенство f(x) < g(x)
x/3 < 6/x
x/3 - 6/x < 0
(x^2 - 18)/3x < 0
1.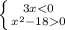 3x < 0 ⇒ x<0 ⇒ x < -
3x < 0 ⇒ x<0 ⇒ x < -
(x + )(x -
)(x -  ) > 0 ⇒ x < -
) > 0 ⇒ x < - или x>
или x>
2.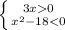 3x > 0 ⇒ x>0
3x > 0 ⇒ x>0
(x + )(x -
)(x -  ) < 0 ⇒ x <
) < 0 ⇒ x <  и x>-
и x>- ⇒ 0<x <
⇒ 0<x < 
x < - и 0<x <
и 0<x < 