





ответ: 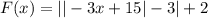
Объяснение:
Попробуем составить функцию с таким графиком. Заметим, что функция имеет форму W, а значит модуль был применен два раза. Заметим, что "уголок" - это часть функции, отраженная относительно OX. Обозначим, нашу показанную функцию как F, на шаге до этого как f1. Тогда:
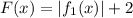
+2 - так как нижние уголки сдвинуты наверх на 2.
Теперь заметим, что высота уголка направленного вверх равна 3. Значит была некоторая функция f2 от которой взяли модуль опустили на 3 и получили f1. Запишем это:
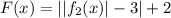
Заметим, что f2 была функцией вида kx+b (примите как факт). Попробуем составить уравнение прямой, которая бы соответствовала рисунку:
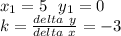
k определяем по наклону левой части графика W. Решаем уравнение:

Отсюда получаем функции:
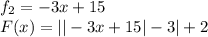
ответ: 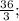 ∞
∞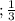
Объяснение:
a)
В этом задании требуется найти определенный интеграл на отрезке x ∈ (1,3). Находим первообразную:
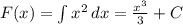
Подставляем в нее границы интегрирования, чтобы найти определенный интеграл:
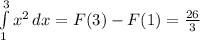
б)
Тоже самое что и в задании а). Находим первообразную функции:
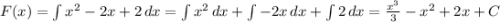
Подставляем в первообразную границы интегрирования. Они определяются через пресечение параболой оси OY:
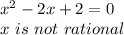
Мы получили, что нет таких точек, которые бы удовлетворяли уравнению, а значит, нет пересечения с OY и площадь ⇒∞.
в)
Находим первообразные для каждой из написанных функций:
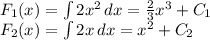
Теперь находим пересечение двух графиков функций. Это и будут границы интегрирования:
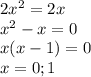
Находим площади под каждой из двух функций при определенного интеграла:
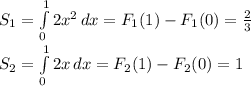
Теперь, чтобы найти общую площадь фигуры вычитаем из большей площади меньшую:
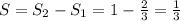
x^2-81=0
x^2=81
|x|=9
совокупность
[x=9
[x=-9
ответ : +-9