Объяснение:
6. данная функция является сложной. корень четной степени - это значит, что значение под корнем должно быть неотрицательным. т.е.
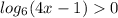решаем данное неравенство.
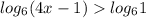
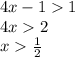
далее, функция логарифмическая, следовательно величина под знаком логарифма должна быть больше нуля.
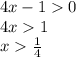
рассматриваем оба неравенства и находим область пересечения интервалов
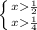x∈ [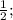 
+∞ [
7. 
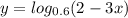значение под знаком логарифма должно быть больше нуля. 2-3х>0 2>3x x<2/3
рассмотрим условие при котором у>1
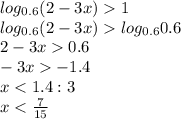
находим область пересечения обоих условий,
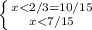x∈ ] -∞; 7/15 [
8. 
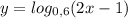область определения функции.
2х-1>0 x>1/2
вводим дополнительное условие
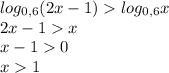
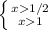x∈ ] 1; +∞ [
Дана функция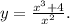 
Производная её равна: y' = (3x^2*x^2 - 2x*(x^3 + 4))/x^4 = (x^3 - 8)/x^3.
Приравняем её нулю ( при х не равном 0 можно только числитель).
x^3 - 8 = 0.
x^3 = 8, х = ∛8 = 2. Это критическая точка.
С учётом разрыва функции при х = 0 имеем 3 промежутка монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На промежутках находим знаки производной.
Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -1 0 1 2 3
y' = 9 - -7 0 0,7037.
• Минимум функции в точке: х = 2, у = 3.
• Максимума функции нет.
• Возрастает на промежутках: (-∞; 0) U (2; ∞).
• Убывает на промежутке: (0; 2).
C=7
Объяснение:
AA+B=C
4+3=7