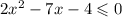
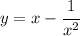параллельно прямой 
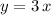будет выглядеть следующим образом: 
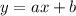, где a - коэффициент наклона касательной, он равен по условию 3, так как прямая параллельна прямой 
.
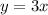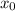равна углу наклона касательной данной функции в этой точке, то, приравняв производную к данному коэффициенту наклона (k = 3), найдем точку касания.
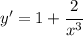. Приравняем её к 3 и получим: 
. 
.
.
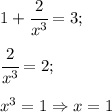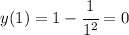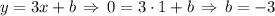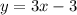
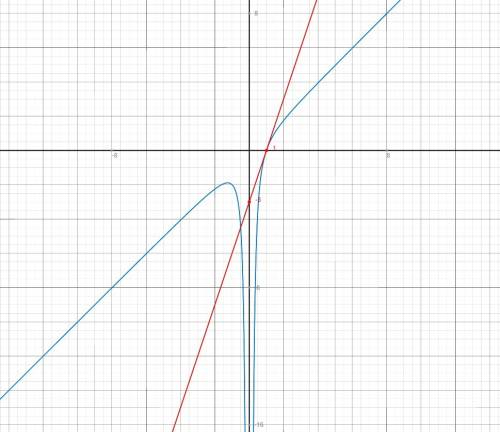
Проведем КР - среднюю линию трапеции.
Проведем MN ║ АВ через точку К. Получим параллелограмм АВMN (противоположные стороны параллельны).
CK = KD по условию,
∠КСМ = ∠KDN как накрест лежащие при ВС║AD и секущей CD,
углы при вершине К равны как вертикальные, значит
ΔСМК = ΔDNK по стороне и двум прилежащим к ней углам, значит
площадь трапеции ABCD равна площади параллелограмма ABMN.
Диагональ делит параллелограмм на два равных треугольника:
Площадь ΔКВР равна половине площади параллелограмма РВМК (верхнего),
площадь ΔКАР равна половине площади параллелограмма АРКN (нижнего), значит
площадь ΔКАВ составляет половину площади всего параллелограмма ABMN, а значит и половину площади трапеции, т.е.
Skab = Sbck + Sadk.