чтобы исследовать функцию на экстремум, надо найти ее производную
у=(х-1)²/х²
это дробь, а производная дроби равна разности произведения производной числителя на знаменатель и произведения числителя на производную знаменателя, деленной на квадрат знаменателя.
у¹ = ((х-1)¹*х² - (х-1)²*(х²)¹)/х⁴= (2х²-2х)/х⁴
у¹=0 - условие экстремума функции
(2х²-2х)/х⁴=0
х≠0 - на ноль делить нельзя
2х²-2х=0
х=0 и х=1 -ноль не подходит, берем 1
Чтобы функция имела в точке экстремум надо, чтобы при переходе через точку она меняла знак
вычислим
у(1/2) = 1 > 0
у(2) = 1/4 > 0
знак не поменялся, значит экстремума в этой точке нет.
в точке х=0, в которой функция не определена тоже нет перемены знака
у(-1) = 4 > 0 и у (1/2) = 1 > 0
ответ: функция экстремумов не имеет.
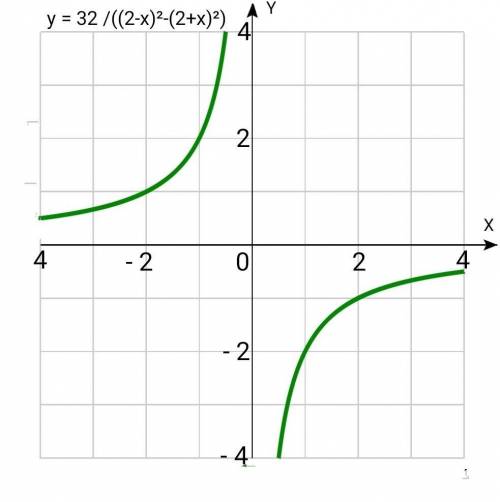
график в прикреплённом изображении.
Объяснение:
у = 32 /((2-х)²-(2+х)²)
1.
Найдём область определения функции:
выражение, записанное в знаменателе дроби, отлично от нуля,
(2-х)²-(2+х)² ≠ 0
(2-х+2+х)(2-х-2-х) ≠ 0
4•(-2х) ≠ 0
-8х ≠ 0
х ≠ 0
хє(-∞;0) ∪ (0; +∞)
2.
у = 32 /((2-х)²-(2+х)²)
у = 32 /(-8х)
у = - 4/х - обратная пропорциональность, графиком является гипербола.
Составим таблицу значений, отметим точки с указанными координатами, соединив их, получим ветви гиперболы:
х l 1 l 2 l 4 l 8 l
y l -4 l -2 l -1 l - 1/2l
Вторая ветвь гиперболы с точками, координаты которых симметричны относительно начала координат.
это раскладывается по формуле а^2-b^2=(a+b)(a-b)
100-b^2=(10-b)(10+b)