Пусть скорость первого велосипедиста равна х км/ч, а второго - у км/ч. Первый и второй велосипедисты проехали 25 км их расстояние (x+у)*1=(x+y) км
На расстоянии 30 км первый велосипедист проезжает на 1 ч быстрее другого,т.е. время затраченное первым велосипедистом равно 30/х, а вторым - 30/у. На весь путь затратили (30/x - 30/y) ч.
Решим систему уравнений
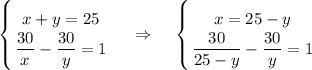
Домножим левую и правую части уравнения на (25-y)y ≠ 0 , получим
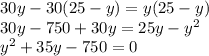
По теореме Виета
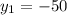 не удовлетворяет условию, так как скорость не может быть отрицательной.
не удовлетворяет условию, так как скорость не может быть отрицательной.
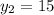 км/ч - скорость второго велосипедиста
км/ч - скорость второго велосипедиста
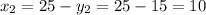 км/ч - скорость первого велосипедиста.
км/ч - скорость первого велосипедиста.
ответ: скорость первого велосипедиста равна 10 км/ч, а второго - 15 км/ч.
task/22381953
Скорость одного велосипедиста обозначаем x км/ч , другого _ y км / ч . * * * Из условия задачи следует ,что x ≠ y , допустим x > y > 0 * * *
До места встречи один км /ч* 1 ч =x км, другой _S₂ =y км/ч*1ч =y км.Один на пути 30 км затрачивает t₁ =30/x час, другой _t₂ = 30 / y час .
Можем составить систему уравнений : { x + y =25 ; 30 / y - 30 / x = 1 .
{ y = 25 - x ; 30 / (25 - x) - 30 / x = 1 .⇔ { y = 25 - x ; 30x -30(25 - x) = x(25 - x ) .
30x - 750 + 30x = 25x - x² ⇔ x² +35x - 750 = 0 ⇒ [ x = 15 ; x = - 50 →.
* * * D = 35² - 4*1*(-750) =1225 +3000 =4225 =65² ; x₁ , ₂ = (-35 ± 65)/2 * * *
у =25 - x =25 -15 = 10 (км/ч) . ответ : 15 км/ч , 10 км/ч .
* * * y² - 85y + 750 = 0 ⇔ [ y = 10 ; y = 75 > 25 →посторонний корень. * * *
1)2xy=5
2x+y=6
Выразим y из второо уравнения:
y=6-2x
Подставим в первое:
2x(6-2x)=5
12x-4x^2 =5
-4x^2+12x-5=0
4x^2 -12x+5
Найдём дискриминант
D=144-5*4*4=64
x1=(12+8)/8=5/2=2,5
x2=(12-8)/8=4/8=1/2=0,5
y1=6-2*2,5)=6-5=1
y2=6-2*0,5=6-1=5
ответ: (2,5; 1), (0,5;5)
2) 3xy=1
6x+y=3
Выразим из второго уравнения у:
y=3-6x
Подставим в первое:
3x(3-6x)=1
9x-18x^2-1=0
18x^2 -9x+1=0
Найдём дискриминант:
D=81-4*18=9
x1=(9+3)/36=12/36=1/3
x2=(9-3)/36=6/36=1/6
y1=3-6*1/3=3-2=1
y2=3-6*1/6=3-1 =2
ответ: (1/3; 1), (1/6; 2)
3) x^2-y=-2
2x+y=2
Вызраим из второго уравнения у:
y=2-2x
Подставим в первое
x^2-2+2x=-2
x^2+2x=0
x(x+2)=0
x1=0 x2=-2
y1=2-2*0=2
y2=2-2(-2)=2+4=6
ответ: (0; 2), (-2; 6)