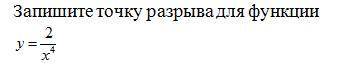

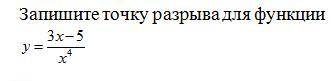
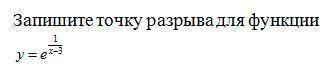
Определение локального максимума и локального минимума
Пусть функция
y
=
f
(
x
)
определена в некоторой
δ
-окрестности точки
x
0
,
где
δ
>
0.
Говорят, что функция
f
(
x
)
имеет локальный максимум в точке
x
0
,
если для всех точек
x
≠
x
0
,
принадлежащих окрестности
(
x
0
−
δ
,
x
0
+
δ
)
,
выполняется неравенство
f
(
x
)
≤
f
(
x
0
)
.
Если для всех точек
x
≠
x
0
из некоторой окрестности точки
x
0
выполняется строгое неравенство
f
(
x
)
<
f
(
x
0
)
,
то точка
x
0
является точкой строгого локального максимума.
Аналогично определяется локальный минимум функции
f
(
x
)
.
В этом случае для всех точек
x
≠
x
0
из
δ
-окрестности
(
x
0
−
δ
,
x
0
+
δ
)
точки
x
0
справедливо неравенство
f
(
x
)
≥
f
(
x
0
)
.
Соответственно, строгий локальный минимум описывается строгим неравенством
если какая-то цифра входит трижды, то другая может входить только единожды
рассмотрим эту возможность
мы можем выбрать любую из 4-х цифр (которая в записи будет единожды), и поставить на любое из 4-х мест, все остальные три цифры "автоматически" заполнятся одной из 3-х оставшихся цифр,
итого по правилу событий всего таких чисел можно составить
4*4*3=48
если все цифры входят в запись числа по одному разу
то на первое место мы можем выбрать одну из 4-х цифр, на второе одну из 3-х оставшихся после выбора цифры на первое место, на третье одну из 2-х оставшихся после выбора на первое и второе, и последняя цифра выбирается "автоматически"
итого по правилу событий всего таких чисел можно составить
4*3*2*1=4!= 24
суммируя получая что всего чисел согласно условию можно составить 48+24=72
ответ: 72 числа