ответ: 2
Объяснение:
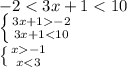
Найдем пересечение
Имеем: x ∈ (-1;3)
Число 3 не входить, тому найбільшим цілим розвязком нерівності є число 2
3х-у=3
{
5х+2у=16
Суть метода сложения в системах уравнений в уничтожении одной переменной, чтобы новое, упрощенное уравнение можно было решить, как обычное (с одной переменной).
Для этого в нашем случае нужно домножить первое уравнение на 2 (2 уравнение оставляем прежним):
6х-2у=6
{
5х+2у=16
Теперь скалдываем подобные:
11х=22
Находим одну переменную (в нашем случае х):
х=2
Подставляем известное значение х в любое из первоначальных уравнений (я подставлю в первое) и решаем как уравнение с одной переменной:
3•2-у=3
6-у=3
-у=-3
у=3
ответ: х=2; у=3.
пусть а - сторона основания, а l - апофема, тогда формула площади поверхности конуса равна 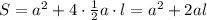
Подставим вместо а и S их значения и найдем апофему l
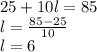
Через апофему проведем сечение пирамиды. В сечении получаем равнобедренный треугольник, основание которого равно стороне а=5, а боковые стороны апофеме l=6. Угол между боковой стороной треугольника и его основанием и есть угол наклона боковой грани пирамиды к плоскости основания. Найдем его, проведем высоту в равнобедренном треугольнике к его основанию. Высота равнобедренного треугольника, проведенная к основанию является так же его биссектрисо и медианой. Поэтому она делит равнобедренный треугольник на два равных прямоугольных треугольника. Найдем косинус искомого угла из прямоугольного треугольника.
Cos A=2,5/6=25/60=5/12 Отсюда следует, что угол наклона боковой грани к плоскости основания пирамиды равен arccos (5/12)
Наибольшее целое решение неравенства - это х=2 .