Объяснение:
15.6
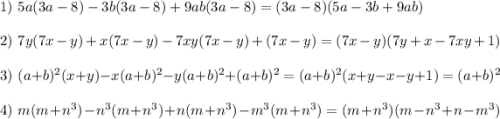
Выносим общую скобку как множитель.
15.9
Тут необходимо сначала разложить на множители, а затем воспользоваться правилом:
Если произведение двух или более множителей равно 0, то хотя бы один из множителей равен 0.
1)
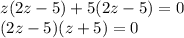
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
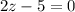 или
или 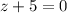
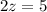 или
или 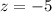
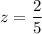 или
или 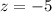
Мы решили! Это и есть ответ!
2)
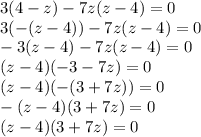
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
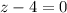 или
или 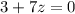
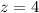 или
или 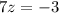
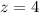 или
или 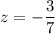
Мы решили! Это и есть ответ!
3)
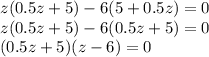
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
 или
или 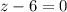
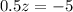 или
или 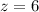
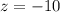 или
или 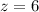
Мы решили! Это и есть ответ!
4)
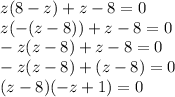
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
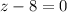 или
или 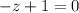
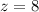 или
или 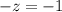
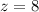 или
или 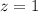
Мы решили! Это и есть ответ!
Объяснение:
15.6
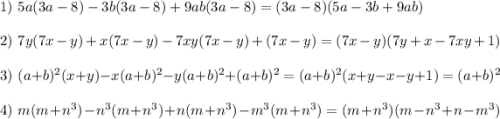
Выносим общую скобку как множитель.
15.9
Тут необходимо сначала разложить на множители, а затем воспользоваться правилом:
Если произведение двух или более множителей равно 0, то хотя бы один из множителей равен 0.
1)
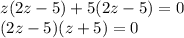
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
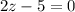 или
или 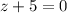
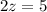 или
или 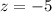
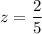 или
или 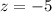
Мы решили! Это и есть ответ!
2)
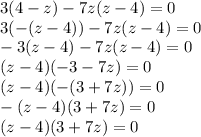
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
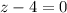 или
или 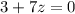
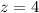 или
или 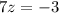
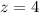 или
или 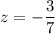
Мы решили! Это и есть ответ!
3)
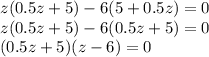
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
 или
или 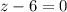
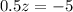 или
или 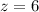
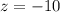 или
или 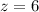
Мы решили! Это и есть ответ!
4)
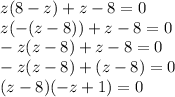
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
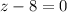 или
или 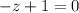
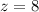 или
или 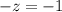
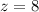 или
или 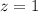
Мы решили! Это и есть ответ!
ответ:Всего
Объяснение:Обратим внимание на то, что требуется сделать букет из 7 цветов так, чтобы в нем было хотя бы три красных тюльпана, а на количество белых тюльпанов ограничений нет. Тогда, заключаем, что в букете
1) в точности 7 тюльпанов;
2) наименьшее количество красных тюльпанов 3;
3) наибольшее количество красных тюльпанов 7.
По условию количество красных тюльпанов в саду 10, то все эти 3 пункта возможны. Обозначим белые тюльпаны через 0, а красные тюльпаны через 1. Так как порядок размещения не даёт новые то получаем следующие
0000111
0001111
0011111
0111111
1111111
Всего