Группа точек имеют одинаковую абсциссу х=4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид .
.
Группа точек имеют одинаковую абсциссу х=2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид .
.
Группа точек имеют одинаковую абсциссу х= -2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид .
.
Группа точек имеют одинаковую абсциссу х= -4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид .
.
Точки, имеющие одинаковую абсциссу, на координатной плоскости лежат на одной прямой, параллельной оси ОУ.
Уравнение такой прямой имеет вид это число (константа- постоянная величина ) .
по условию пирамида правильная треугольная, => основание высоты пирамиды - центр описанной около треугольника окружности - точка пересечения высот правильного треугольника, которые точкой пересечения делятся в отношении 2:1 считая от вершины.
прямоугольный треугольник: гипотенуза с=5 см - длина бокового ребра правильной треугольной пирамиды катет а=3 см - высота правильной пирамиды катет b найти, по теореме Пифагора: 5²=3²+b². b=4 см
b- (1/3) высоты правильного треугольника, которая вычисляется по формуле: a=8/√3
Группа точек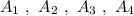
имеют одинаковую абсциссу х=4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
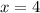Группа точек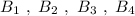
имеют одинаковую абсциссу х=2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
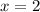Группа точек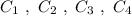
имеют одинаковую абсциссу х= -2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
Группа точек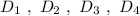
имеют одинаковую абсциссу х= -4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
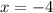Точки, имеющие одинаковую абсциссу, на координатной плоскости лежат на одной прямой, параллельной оси ОУ.
Уравнение такой прямой имеет вид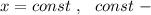
это число (константа- постоянная величина ) .