Пусть х - меньшая сторона прямоугольника, тогда (х+3) - большая сторона:
15^2=(x+3)^2 + x^2
225=x^2+6x+9+x^2
2x^2+6x-216=0
D=36+1728+1764; Корень квадратный из D = 42
x1= (-6-42)/4=-12 - не является решением задачи, т.к. сторона прямоугольника не может быть равна отрицательному числу
х2 = (-6+42)/4=9 - меньшая сторона прямоугольника
9+3+12 - большая сторона прямоугольника
S = 9*12=108 кв. см
ответ: 108 кв. см
Задача 2.
Пусть сторона квадрата равна х, тогда:
x^2 +x^2 = (10*корень из 2)^2
2x^2=200
x^2=100
x = 10 - сторона квадрата
Периметр равен 10*4=40
ответ 40
Пусть х - меньшая сторона прямоугольника, тогда (х+3) - большая сторона:
15^2=(x+3)^2 + x^2
225=x^2+6x+9+x^2
2x^2+6x-216=0
D=36+1728+1764; Корень квадратный из D = 42
x1= (-6-42)/4=-12 - не является решением задачи, т.к. сторона прямоугольника не может быть равна отрицательному числу
х2 = (-6+42)/4=9 - меньшая сторона прямоугольника
9+3+12 - большая сторона прямоугольника
S = 9*12=108 кв. см
ответ: 108 кв. см
Задача 2.
Пусть сторона квадрата равна х, тогда:
x^2 +x^2 = (10*корень из 2)^2
2x^2=200
x^2=100
x = 10 - сторона квадрата
Периметр равен 10*4=40
ответ 40
В решении.
Объяснение:
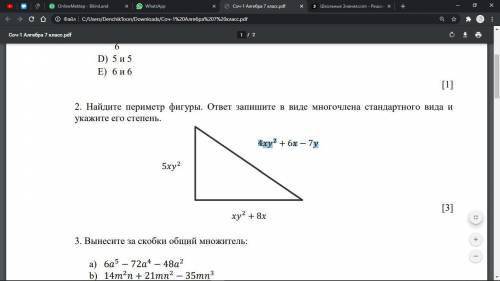
2) Сложить длины всех сторон:
4ху²+6х-7у+5ху²+ху²+8х=
=10ху²+14х-7у (запись в стандартном виде, т.е., по мере убывания степеней);
Степенью многочлена называют наибольшую из степеней входящих в него одночленов.
Здесь: ху²= 1+2=3;
Наибольшая степень 3, это степень многочлена.
3) Вынести общий множитель за скобки:
а) 6а⁵ - 72а⁴ - 48а² = 6а² * (а³ - 12а² - 8);
б) 14m²n + 21mn² - 35mn³ = 7mn * (2m + 3n - 5n²).