Функция f(x)=4x³+8x²+9;
а) найти промежутки возврастания(убывания) ;
б ) найти критические точки .
f '(x) = (4x³+8x²+9) ' =(4x³) ' +(8x²) '+( 9) '=4(x³) ' +8(x²) '+0 =4*3x² +8*2x =
12x(x+4/3) ; D(f '(x) ) : x ∈ R
Функция убывает (↓) ,если f '(x) ≤ 0 ( возрастает, если f '(x) ≥ 0 )
12(x+4/3)x ≤ 0 ⇒ x∈ [ - 4/3 ; 0 ]
[ - 4/3 ] [0]
f ' (x) "+" " -" " +"
f(x) ↑ ↓ ↑
Функция возрастает промежутках ( -∞ ; -4/3] и [ 0 ; ∞) ;
убывает в промежутке [ - 4/3 ; 0]
- - - - - - -
б) Критические точки : f '(x) = 0 ⇔ (x+4/3)x =0 ⇒ x = - 4/3 и x=0 , притом эти критические точки являются точками экстремумов .
x = - 4/3 точка максимума ; x=0 _точка минимума.
Скорость грузовой машины - 40км/ч.
Выразим скорость грузовой машины через х. Тогда скорость легковой машины - 1,5х (км/ч). Сколько времени ехала грузовая машина?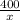
часов. А легковая, соответственно, 
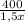часов. Поскольку известно, что выехала она на 2 часа позже, а приехала на 
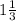часа раньше, значит, в целом она пробыла в пути на 
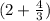часов меньше.
Составим уравнение:
Избавимся от знаменателей, умножив обе части на общий множитель 3х.
Получим: 800 = 1200 - 10х
10х=400
х=40.
А это и есть скорость грузовика